当前位置：试卷中心 > 试卷详情

2022-2023学年福建省福州四中桔园洲中学九年级（上）第四次适应性数学试卷

发布：2024/9/11 7:0:8

一、选择题

1．下列航天图标中，其图案是中心对称图形的是（　　）
A． B． C． D．
组卷：121引用：9难度：0.9
解析

2．下列事件中，是随机事件的是（　　）

A．福州第四中学桔园洲中学第17届运动会没有在2022年进行

B．福州市2023年九上期末适应性练习没有如期进行

C．福州第四中学桔园洲中学2023年九上期末适应性练习如期进行

D．掷一枚硬币，正面朝上

组卷：13引用：2难度：0.5

解析

3．将抛物线y=x²向上平移1个单位，就得到抛物线（　　）
A．y=x²+1 B．y=（x+1）² C．y=x²-1 D．y=（x-1）²
组卷：85引用：6难度：0.7
解析
4．反比例函数y=
k
x
（k≠0）的图象经过点（-2，3），则该反比例函数图象在（　　）
A．第一，三象限 B．第二，四象限
C．第二，三象限 D．第一，二象限
组卷：234引用：45难度：0.9
解析
5．如图所示，在⊙O中，
ˆ
AB
=
ˆ
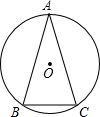AC
，∠A=30°，则∠B=（　　）
A．150° B．75° C．60° D．15°
组卷：4115引用：64难度：0.9
解析
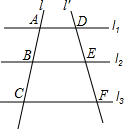6．如图，直线l₁∥l₂∥l₃，若AB=3，BC=4，则
DE
DF
的值是（　　）
A．
7
3
B．
3
7
C．
4
3
D．
4
7
组卷：310引用：5难度：0.9
解析
7．边长为2的正六边形的外接圆半径是（　　）
A．1 B．
3
C．2 D．
2
3
组卷：17引用：3难度：0.5
解析
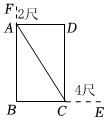8．陈老师和与她搭班的李老师都十分热爱文学．某日，陈老师翻阅到一本古代数学著作—《增删算法统宗》，看到里面记载了这样一个问题：“今有门厅一座，不知门广高低，长午横进使归室，争奈门狭四尺，随即竖竿过去，亦长二尺无疑，两隅斜去恰方齐，请问三色各几？”．为了能够更通顺地读懂这个问题，陈老师找了李老师勾兑一二，最后得到了其可能的大意：“今有一房门，不知宽与高，长竿横着进门，门的宽度比竿小4尺进不了；将竿竖着进门，竿比门长2尺；将竿斜着穿过门的对角，恰好进门．试问门的宽、高和竿长各是多少？”根据翻译，她画出了这样一幅图，并设竿长AC为x尺，则下列方程中符合题意的是（　　）
A．（x-4）²+（x-2）²=x² B．4²+（x-2）²=x²
C．（x-4）²+（x-2）²=2x² D．（x-4）²+2²=x²
组卷：18引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

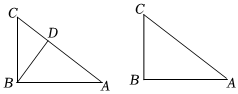24．如图，在Rt△ABC中，∠ABC=90°，BD⊥AC于点D．
（1）求证：△ABD∽△ACB；
（2）将△ABD绕点A顺时针旋转α（0°＜α＜180°）得到△AEF，其中E是点B的对应点．连接CE，取CE中点G，连接GB，GF．
①求证：GB=GF；
②连接BF，若AB=4，BC=3，求△BGF面积的最大值．
组卷：15引用：2难度：0.1
解析
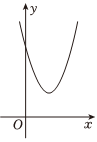25．已知抛物线C：y=x²-4x+c,直线l：y=mx（m＞0）．当m=1时，直线l恰好经过抛物线C的顶点．
（1）求抛物线C的解析式；
（2）若直线l与抛物线C交于不同的两点A，B（点A在点B左侧），线段AB与直线l₁：y=kx+b交于一点P（横坐标为x_P）．对于任意常数t（t＞0），不论m取何值都有
1
OA
+
1
OB
=
t
OP
成立，求k的值；
（3）在（2）的条件下，设直线l₁与y轴交于点Q，当存在m使得S_△APQ=S_△BPQ成立时，求点P横坐标x_P的取值范围．
组卷：18引用：2难度：0.5
解析