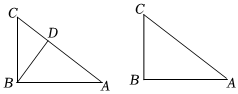
如图，在Rt△ABC中，∠ABC=90°，BD⊥AC于点D．
（1）求证：△ABD∽△ACB；
（2）将△ABD绕点A顺时针旋转α（0°＜α＜180°）得到△AEF，其中E是点B的对应点．连接CE，取CE中点G，连接GB，GF．
①求证：GB=GF；
②连接BF，若AB=4，BC=3，求△BGF面积的最大值．
【考点】相似形综合题．
【答案】（1）证明见解析；
（2）①证明见解析；②．
（2）①证明见解析；②
243
25
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/11 7:0:8组卷：15引用：2难度：0.1
相似题
-
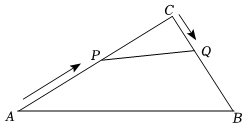1．在Rt△ABC中，∠C=90°，AC=40cm,BC=30cm.现有动点P从点A出发，沿线段AC向点C方向运动：动点Q从点C出发，沿线段CB向点B方向运动．如果点P的速度是8cm/s,点Q的速度是4cm/s,它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为t秒．求：
（1）当t=3时，P、Q两点之间的距离是多少？
（2）若△CPQ的面积为S，求S关于t的函数关系式．
（3）当t为多少时，以点C，P，Q为顶点的三角形与△ABC相似？发布：2025/5/24 11:0:1组卷：123引用：2难度：0.2 -
2．如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为倍角三角形，并称这两个角的公共边为底边．
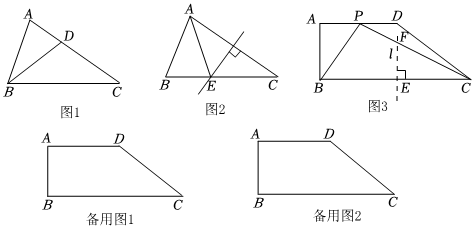
例如：若△ABC中，∠A=2∠B，则△ABC为以边AB为底边的倍角三角形．
（1）已知△ABC为倍角三角形，且∠ABC=2∠C．
①如图1，若BD为△ABC的角平分线，则图中相等的线段有 ，图中相似三角形有 ；
②如图2，若AC的中垂线交边BC于点E，连接AE，则图中等腰三角形有 ．
问题解决
（2）如图3，现有一块梯形板材ABCD，AD∥BC，∠A=90°，AB=48，BC=132，AD=68．工人师傅想用这块板材裁出一个△BCP型部件，使得点P在梯形ABCD的边上，且△BCP为以BC为底边的倍角三角形．工人师傅在这块板材上的作法如下：
①作BC的中垂线l交BC于点E；
②在BC上方的直线l上截取EF=33，连接CF并延长，交AD于点P；
③连接BP，得△BCP．
1）请问，若按上述作法，裁得的△BCP型部件是否符合要求？请证明你的想法．
2）是否存在其它满足要求的△BCP？若存在，请画出图形并求出CP的长；若不存在，请说明理由．发布：2025/5/24 13:30:2组卷：255引用：4难度：0.1 -
3．（1）问题发现
如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M，填空：的值为；∠AMB的度数为，ACBD
（2）类比探究
如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD的延长线于点M，请判断的值及∠AMB的度数，并说明理由．ACBD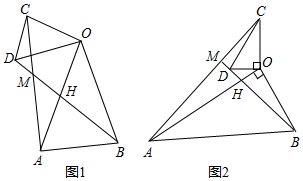
发布：2025/5/24 12:30:1组卷：917引用：7难度：0.3
