当前位置：试卷中心 > 试卷详情

2022-2023学年广东省东莞市高一（下）期末数学试卷

发布：2024/6/10 8:0:9

一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．请把正确选项在答题卡中的相应位置涂黑．

1．复数
（
i
i
+
1
）
2
（i是虚数单位）等于（　　）
A．
i
2
B．
-
i
2
C．
1
2
D．
-
1
2
组卷：45引用：1难度：0.8
解析
2．已知向量
a
=
（
1
，
2
）
，
b
=
（
λ
，
4
）
，且
a
∥
b
，则
|
a
+
b
|
=（　　）
A．
5
B．
15
C．
3
5
D．
13
组卷：111引用：1难度：0.8
解析
3．利用随机模拟解决问题的方法称为蒙特卡洛方法，用此方法可以快速进行大量重复试验，进而用频率估计概率．甲、乙两名选手进行比赛，采用三局两胜制决出胜负，若每局比赛甲获胜的概率为0.4，乙获胜的概率为0.6．利用计算机产生1～5之间的随机整数，约定出现随机数1或2时表示一局比赛甲获胜，由于要比赛3局，所以3个随机数为一组，现产生了20组随机数如下：
354 151 314 432 125 334 541 112 443 534 312 324 252 525 453 114 344 423 123 243，则依此可估计甲选手最终赢得比赛的概率为（　　）
A．0.40 B．0.35 C．0.30 D．0.25
组卷：100引用：4难度：0.8
解析
4．已知不重合的直线l,m和不重合的平面α，β，下列命题正确的是（　　）
A．若l∥α，l∥β，则α∥β
B．若α∩β=l,m⊂α，m⊥l,则α⊥β
C．若l⊥α，l⊥β，则α∥β
D．若l⊂α，m⊂β，l⊥m,则α⊥β
组卷：96引用：1难度：0.7
解析
5．平均数和中位数都描述了数据的集中趋势，它们的大小关系和数据分布的形态有关．下面四幅频率分布直方图中，最能说明平均数大于中位数的是（　　）
A． B．
C． D．
组卷：136引用：4难度：0.8
解析
6．正方体ABCD-A₁B₁C₁D₁中，与AC所成角为60°的直线是（　　）
A．A₁B₁ B．AC₁ C．BD₁ D．C₁D
组卷：68引用：1难度：0.5
解析
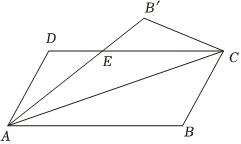7．如图，在平行四边形ABCD中，AB=2，BC=1，∠DAB=
π
3
，将三角形ABC沿AC翻折得三角形AB'C，使得AB'交CD于E，则DE=（　　）
A．
2
3
B．
3
5
C．
3
4
D．
4
5
组卷：71引用：1难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本大题共6小题，第17题10分，18、19、20、21、22题各12分，共70分．解答应写出文字说明、证明过程或演算步骤，必须把解答过程写在答题卡相应题号指定的区域内，超出指定区域的答案无效．

21．树人中学男女学生比例约为2：3，某数学兴趣社团为了解该校学生课外体育锻炼情况（锻炼时间长短（单位：小时），采用样本量比例分配的分层抽样，抽取男生m人，女生n人进行调查．记男生样本为x₁，x₂，…，x_m，样本平均数、方差分别为
x
、
s
2
1
；女生样本为y₁，y₂，…，y_n，样本平均数、方差分别为
y
、
s
2
2
；总样本平均数、方差分别为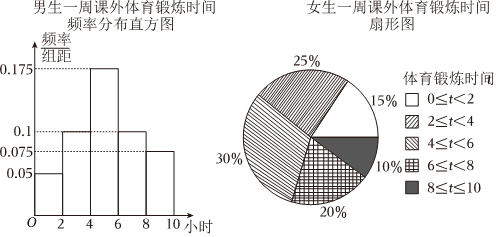
w
、s²．

（1）证明：
m
∑
i
=
1
（
x
i
-
w
）
2
=
m
[
s
2
1
+
（
x
-
w
）
2
]
；
（2）该兴趣社团通过分析给出以下两个统计图，假设两个统计图中每个组内的数据均匀分布，根据两图信息分别估计男生样本、女生样本的平均数；
（3）已知男生样本方差
s
2
1
=5.5，女生样本方差
s
2
2
=5.7，请结合（2）问的结果计算总样本方差s²的估计值．
组卷：81引用：1难度：0.6
解析
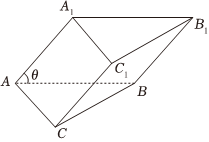22．如图，在三棱柱ABC-A₁B₁C₁中，底面ABC是边长为2的等边三角形，平面A₁ABB₁⊥平面ABC，
A
A
1
=
2
，∠A₁AB=θ．
（1）当
θ
=
π
4
时，求异面直线AC与BB₁所成角的余弦值；
（2）若存在球与三棱柱ABC-A₁B₁C₁各个面都相切，求θ的正弦值．
组卷：172引用：1难度：0.5
解析