当前位置：试卷中心 > 试卷详情

2023年湖南省益阳十五中中考数学模拟试卷

发布：2024/6/13 8:0:9

一、选择题（本题共10个小题，每小题4分，共40分．每小题给出的四个选项中，只有一项是符合题目要求的）

1．在|-1|，
3
27
，π，
2
这四个数中最大的数是（　　）
A．|-1| B．
3
27
C．π D．
2
组卷：150引用：2难度：0.7
解析
2．下列计算正确的是（　　）
A．（a²）³=a⁵ B．a³+a=2a⁴
C．a⁸÷a²=a⁶ D．（-5a²b）（-3a）=15a²b
组卷：237引用：2难度：0.8
解析
3．已知点P（2n-7，4-2n）在第二象限，则n的取值范围是（　　）
A．n＜2 B．n＞2 C．n＜
7
2
D．2＜n＜
7
2
组卷：123引用：3难度：0.7
解析
4．已知关于x的方程x²+px+q=0的两根为-3和2，则
q
p
的值为（　　）
A．-6 B．
-
1
6
C．
1
6
D．6
组卷：230引用：2难度：0.7
解析
5．已知直线y=kx-4与两坐标轴所围成的三角形面积等于4，则直线的解析式为（　　）
A．y=2x-4 B．y=-2x-4
C．
y
=
1
2
x
-
4
D．y=2x-4或y=-2x-4
组卷：355引用：2难度：0.7
解析
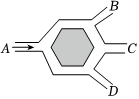6．如图，A是某公园的进口，B，C，D是三个不同的出口，小明从A处进入公园，那么在B，C，D三个出口中恰好从B出口出来的概率为（　　）
A．
1
4
B．
1
3
C．
1
2
D．
2
3
组卷：599引用：8难度：0.8
解析
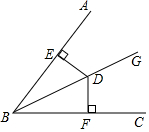7．如图，已知BG是∠ABC的平分线，DE⊥AB于点E，DF⊥BC于点F，DE=6，则DF的长度是（　　）
A．2 B．3 C．4 D．6
组卷：3299引用：27难度：0.9
解析
8．若关于x的不等式组
x
-
3
2
＜
2
x
-
3
4
+
1
2
（
x
-
1
18
a
）
≥
5
3
x
的所有整数解的和为5，且使关于y的分式方程
2
y
y
-
2
=3+
a
2
-
y
的解大于1，则满足条件的所有整数a的和是（　　）
A．6 B．11 C．12 D．15
组卷：403引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共8个小题，共78分，解答应写出文字说明、证明过程或演算步骤）

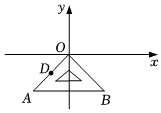25．如图，某数学小组以等腰直角三角形OAB纸板的直角顶点O为坐标原点，建立平面直角坐标系，已知点A（-2，-2），B（2，-2），请思考并解决下列问题：
（1）若抛物线C₁过三点O、A、B，求此抛物线的表达式；
（2）设OA的中点为D，若抛物线经过平移顶点为D，写出平移后的抛物线C₂的解析式．若点P（m,y₁），Q（1，y₂）是抛物线C₂上两点，当y₁＞y₂时，求m的取值范围；
（3）将△OAB沿水平方向平移，当恰好有一个顶点落在抛物线C₂上时，请直接写出平移的距离．
组卷：232引用：3难度：0.4
解析
26．如图1，在平面直角坐标系中，直线y=-
3
4
x+n分别与x轴、y轴交于点A、B，且点A的坐标为（4，0），点C为线段AB的中点．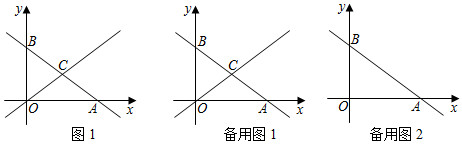

（1）求点B的坐标；
（2）点P为直线AB上的一个动点，过点P作x轴的垂线，与直线OC交于点Q，设点P的横坐标为m,△OPQ的面积为S，求S与m的函数解析式；
（3）当点P在直线AB上运动时，在平面直角坐标系内是否存在一点N，使得以O，B，P，N为顶点的四边形为矩形，若存在，求出N点的坐标；若不存在，请说明理由．
组卷：828引用：6难度：0.4
解析