2022-2023学年山西省朔州市八年级（下）期末数学试卷

一、选择题（本大题共10个小题，每小题3分，共30分，在每个小题给出的四个选项中，其中只有一项是符合题意的）

• 1．正比例函数

  y

  =

  1

  4

  x

  的图象经过（　　）

  A．第一、二象限	B．第一、三象限
  C．第一、四象限	D．第二、四象限
  组卷：215引用：4难度：0.7

  解析

• 2．若▱ABCD的相邻两边长为4cm和2cm,则该▱ABCD的周长为（　　）

  A．12cm

  B．10cm

  C．8cm

  D．6cm
  组卷：31引用：1难度：0.9

  解析

• 3．近年来，中国北斗芯片实现了22纳米制程的突破，领先GPS芯片．已知22纳米=0.000000022米，数据0.000000022用科学记数法可表示为（　　）

  A．0.22×10-7

  B．2.2×10-8

  C．2.2×10-9

  D．22×10-9
  组卷：545引用：16难度：0.8

  解析

• 4．化简

  x

  2

  -

  1

  x

  +

  1

  的结果是（　　）

  A．x+1

  B． x x + 1

  C．x-1

  D． 1 x + 1
  组卷：175引用：1难度：0.7

  解析

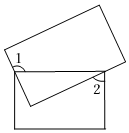• 5．两个矩形的位置如图所示，若∠1=115°，则∠2=（　　）

  A．50°

  B．55°

  C．60°

  D．65°
  组卷：43引用：1难度：0.5

  解析

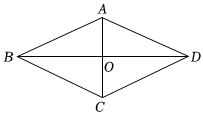• 6．如图，在菱形ABCD中，对角线AC，BD相交于点O，若

  AB

  =

  5

  ，AC=2，则BD的长为（　　）

  A．8

  B．6

  C．4

  D．2
  组卷：64引用：1难度：0.5

  解析

• 7．小明家计划利用一堵长为8m的墙，用篱笆围一个面积为48m²的矩形养鸡场ABCD．如图，设AB的长为x（m），BC的长为y（m），则y关于x的函数关系式为（包括自变量x的取值范围）（　　）
  ​

  A． y = 48 x （x≥6）

  B．y=48x（x≥6）

  C．y= 48 x （ x ≤ 6 ）

  D．y=48x（x≤6）
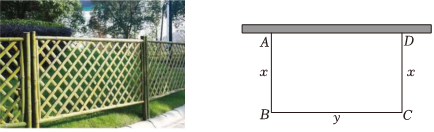  组卷：187引用：3难度：0.8

  解析

三、解答题（本大题共8个小题，共75分，解答应写出必要的文字说明，证明过程或演算步骤）

• 21．综合与实践
  在正方形ABCD中，Q为正方形ABCD边上一点，过点B，Q作直线MN，过点A，C，D分别作AE⊥MN、CF⊥MN，DG⊥MN，垂足分别是E，F，G．
  【思考证明】如图1，当Q是边AD上的点时，过点D作DH∥MN，交CF于点H．
  （1）试判断四边形DHFG的形状，并加以证明．
  （2）求证：FG=BE．
  【问题拓展】
  （3）如图2．当Q是边CD上的点时，其他条件不变，若AE=3DG+2，CF=16，请直接写出DG的长．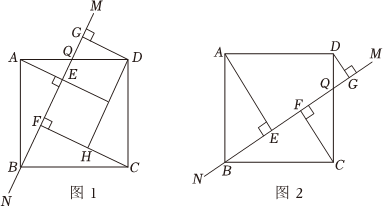
  ​
  组卷：51引用：1难度：0.3

  解析

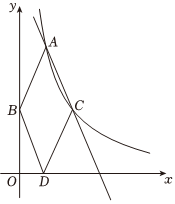• 22．综合与探究
  如图，反比例函数

  y

  =

  m

  x

  （

  x

  ＞

  0

  ）

  的图象与一次函数y=kx+b（k≠0）的图象交于点A（n,4），C（m-1，2），作直线AC．
  （1）求反比例函数

  y

  =

  m

  x

  （

  x

  ＞

  0

  ）

  和一次函数y=kx+b（k≠0）的表达式；
  （2）根据函数的图象，直接写出不等式

  m

  x

  ＞

  kx

  +

  b

  的解集；
  （3）在y轴上有一点B，若点B的坐标为（0，2），连接AB，过点C作CD∥AB交x轴于点D，连接BD．试判断四边形ABDC的形状，并说明理由．
  ​
  组卷：69引用：1难度：0.5

  解析