2022-2023学年湖北省黄冈市红安县八年级（下）期末数学试卷

一、选择题（共8小题）（每小题3分，共24分）

• 1．下列式子一定是二次根式是（　　）

  A． m

  B． - 5

  C． a 2 + 1

  D． 3 27
  组卷：72引用：1难度：0.8

  解析

• 2．下面各组数是三角形三边的长，能构成直角三角形的是（　　）

  A．4，6，8

  B．5，11，13

  C．6，7，9

  D．7，24，25
  组卷：28引用：1难度：0.7

  解析

• 3．一组数据：7，13，11，16，8，9，9，17，这组数据的中位数和众数是（　　）

  A．11，9

  B．10，9

  C．9，9

  D．9，13
  组卷：48引用：1难度：0.7

  解析

• 4．如图，四边形ABCD中，对角线AC，BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（　　）

  A．AB=DC，AD=BC	B．∠DAB=∠DCB，∠ABC=∠ADC
  C．AO=CO，BO=DO	D．AB∥CD，AD=BC
  组卷：726引用：10难度：0.8

  解析

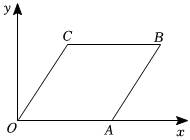• 5．如图，在平面直角坐标系xOy中，菱形OABC的边OA在x轴上，∠B=60°，点A的坐标是（4，0），则B的坐标为（　　）

  A．（5， 2 3 ）

  B． （ 6 ， 2 3 ）

  C．（6，4）

  D．（5，4）
  组卷：52引用：1难度：0.5

  解析

• 6．在同一平面直角坐标系中，一次函数y=ax+b的图象与正比例函数y=

  b

  a

  x图象的位置不可能是（　　）

  A．

  B．

  C．

  D．
  组卷：482引用：4难度：0.8

  解析

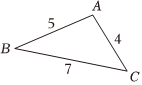• 7．古希腊几何学家海伦在他的著作《度量》中，给出了计算三角形面积的海伦公式，若一个三角形三边长分别为a、b、c,记

  p

  =

  a

  +

  b

  +

  c

  2

  ，三角形的面积为s=

  p

  （

  p

  -

  a

  ）

  （

  p

  -

  b

  ）

  （

  p

  -

  c

  ）

  ，如图，请你利用海伦公式计算△ABC的面积为（　　）

  A． 4 6

  B． 15 2 7

  C． 15 4 6

  D．3 7
  组卷：85引用：1难度：0.7

  解析

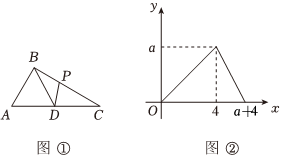• 8．如图①，在Rt△ABC中，∠ABC=90°，D是斜边AC的中点，动点P从C点出发，沿C→B→D运动，设S_△DPC=y,点P运动的路程为x,若y与x之间的函数图象如图②所示，则△ABC的面积为（　　）

  A． 2 3

  B． 4 3 3

  C． 8 3 3

  D．4
  组卷：44引用：1难度：0.5

  解析

三.解答题（共8小题，共72分）

• 23．【建立模型】如图①，等腰直角三角形△ABC的直角顶点B在线段EF上，过点A作AE⊥EF于点E，过点C作CF⊥EF于点F，可以得到结论：△ABE≌△BCF．
  【运用模型】请利用这一结论解决下列问题：
  （1）如图①，请证明△ABE≌△BCF；
  （2）如图②，在平面直角坐标系中，A（1，0），C（-1，4），过点A作AB⊥AC，使AB=AC，请直接写出点B的坐标．
  （3）如图③，在平面直角坐标系中，点A的坐标为（-2，6），点B的坐标为（6，2），第一象限内是否存在一点P，使△ABP为等腰直角三角形？如果存在，请求出点P的坐标．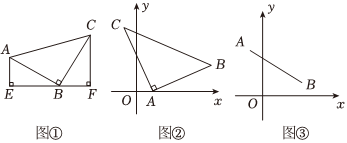
  
  组卷：610引用：3难度：0.2

  解析

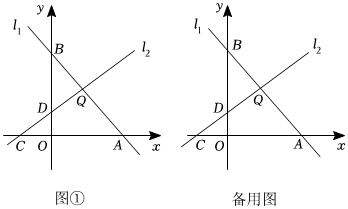• 24．如图，在平面直角坐标系中，直线l₁：y=kx+8分别交x轴，y轴于点A，B，点A（8，0）．直线l₂：

  y

  =

  1

  2

  x

  +

  b

  经过线段AB的中点Q，分别交x轴，y轴于点C，D．
  （1）请直接写出k的值；
  （2）请求出直线l₂的解析式；
  （3）点P（t,0）为x轴上一动点，过点P作PE∥y轴交l₁，l₂于点E，F；
  ①当EF=2EP时，求t的值．
  ②连接BC，当∠OBC=∠ABF时，求t的值．
  组卷：120引用：1难度：0.3

  解析