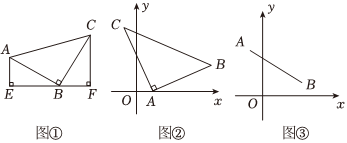
【建立模型】如图①，等腰直角三角形△ABC的直角顶点B在线段EF上，过点A作AE⊥EF于点E，过点C作CF⊥EF于点F，可以得到结论：△ABE≌△BCF．
【运用模型】请利用这一结论解决下列问题：
（1）如图①，请证明△ABE≌△BCF；
（2）如图②，在平面直角坐标系中，A（1，0），C（-1，4），过点A作AB⊥AC，使AB=AC，请直接写出点B的坐标．
（3）如图③，在平面直角坐标系中，点A的坐标为（-2，6），点B的坐标为（6，2），第一象限内是否存在一点P，使△ABP为等腰直角三角形？如果存在，请求出点P的坐标．
【考点】三角形综合题．
【答案】（1）证明见解析；
（2）（5，2）；
（3）第一象限内存在一点P，使△ABP为等腰直角三角形，点P的坐标为（2，14）或（10，10）或（4，8）．
（2）（5，2）；
（3）第一象限内存在一点P，使△ABP为等腰直角三角形，点P的坐标为（2，14）或（10，10）或（4，8）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/4 8:0:9组卷：614引用：3难度：0.2
相似题
-
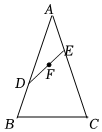1．如图，△ABC是等腰三角形，AB=AC=5，∠BAC是锐角．点D从点A向点B运动，点E是AC上一动点，在运动过程中保持AD=CE，连接DE，若，则在点D运动的过程中，线段DE的中点F的运动路径长是 ．S△ABC=152发布：2025/5/25 17:0:1组卷：127引用：1难度：0.4 -
2．如图，在△ABC中，∠BAC=90°，AB=AC，点D在边AC上，点E在线段BD上，连接AE，且AE=BE，延长AE交BC于点F，过点A作AG⊥AE交BD的延长线于点G．
（1）①若∠GBC=30°，则∠AEG=°；②如图1，求证：∠AGB=2∠GBC；
（2）如图2，连接CG，若∠BGC=90°，求证：BG平分∠ABC；
（3）如图3，若AF=AG，求证：D是AC的中点．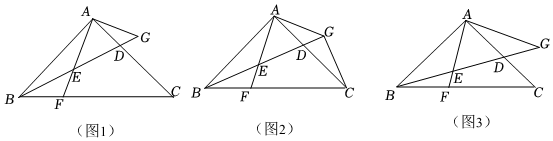
发布：2025/5/25 17:0:1组卷：201引用：1难度：0.3 -
3．已知：在△ABC中，AB=AC，∠BAC=120°，点F是线段BC上一点，D、E是射线AF上两点，且∠ADB=∠BAC，∠AEC=60°．
（1）如图1，
①填空：∠BAE ∠ACE；（填“＞”或“=”或“＜”）
②判定三条线段AD，BD，CE的数量关系，并说明理由；
（2）若∠DBC=15°，则直接写出的值．FCBF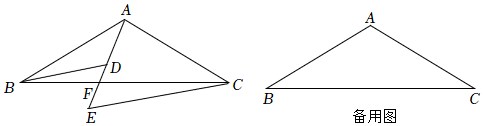
发布：2025/5/25 17:30:1组卷：278引用：3难度：0.1
