2023-2024学年湖北省武汉二中高二(上)段考数学试卷(10月份)
发布:2024/9/16 0:0:8
一.单选题(共8小题)
-
1.圆x2+y2+4x-1=0关于点(0,0)对称的圆的标准方程为( )
组卷:570引用:7难度:0.7 -
2.直线l1:mx-3y-1=0,l2:(3m-2)x-my+2=0,若l1⊥l2,则实数m的值为( )
组卷:328引用:8难度:0.8 -
3.若圆心在第一象限的圆过点(2,0),且与两坐标轴都相切,则圆心到直线2x+y-11=0的距离为( )
组卷:171引用:3难度:0.5 -
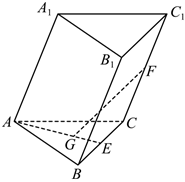 4.如图,在三棱柱ABC-A1B1C1中,E、F分别是BC、CC1的中点,G为△ABC的重心,则=( )GF组卷:671引用:11难度:0.8
4.如图,在三棱柱ABC-A1B1C1中,E、F分别是BC、CC1的中点,G为△ABC的重心,则=( )GF组卷:671引用:11难度:0.8 -
5.设a,b为实数,若直线ax+by=1与圆x2+y2=1相交,则点P(a,b)与圆的位置关系是( )
组卷:318引用:9难度:0.7 -
6.已知直线l:y=k(x-2)+3,且l与x轴、y轴分别交于A、B两点.若使△AOB的面积为12的直线l共有( )条.
组卷:79引用:1难度:0.5 -
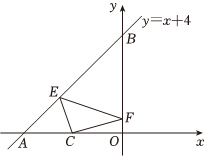 7.如图,一次函数y=x+4的图象与x轴,y轴分别交于点A,B,点C(-2,0)是x轴上一点,点E,F分别为直线y=x+4和y轴上的两个动点,当△CEF周长最小时,点E,F的坐标分别为( )组卷:548引用:7难度:0.8
7.如图,一次函数y=x+4的图象与x轴,y轴分别交于点A,B,点C(-2,0)是x轴上一点,点E,F分别为直线y=x+4和y轴上的两个动点,当△CEF周长最小时,点E,F的坐标分别为( )组卷:548引用:7难度:0.8
四.解答题(共6小题)
-
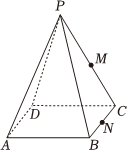 21.如图所示,四棱锥的底面ABCD为边长为的正方形,且PA=PB=PC=PD=2,M为棱PC的中点,N为棱BC上的点.2
21.如图所示,四棱锥的底面ABCD为边长为的正方形,且PA=PB=PC=PD=2,M为棱PC的中点,N为棱BC上的点.2
(1)求直线AM与平面BMD所成角的余弦值;
(2)线段BC上是否存在一点N,使得平面DMN与平面BMD夹角的余弦值为,若存在,求出BN长度.155组卷:31引用:1难度:0.5 -
22.已知圆M的圆心M在x轴上,半径为2,直线l:3x+4y-1=0被圆M截得的弦长为
,且圆心M在直线l的上方.23
(1)求圆M的方程;
(2)设A(0,t),B(0,t-6)(2≤t≤4),若圆M是△ABC的内切圆,求AC,BC边所在直线的斜率(用t表示);
(3)在(2)的条件下求△ABC的面积S的最大值及对应的t值.组卷:43引用:2难度:0.6


