2023-2024学年辽宁省本溪十二中九年级(上)期中数学试卷
发布:2024/10/3 7:0:1
一、选择题(下列各题的备选答案中,只有一个答案是正确的.每小题2分,共20分)
-
1.把一元二次方程(x-2)(x+3)=1化成一般形式,正确的是( )
组卷:619引用:6难度:0.5 -
2.下列说法错误的是( )
组卷:220引用:5难度:0.8 -
 3.如图,点O,F在直线AD上,点O,E在直线BC上,且AB∥EF∥CD,若AO=2,OF=1,FD=2,则的值为( )BEEC组卷:835引用:8难度:0.7
3.如图,点O,F在直线AD上,点O,E在直线BC上,且AB∥EF∥CD,若AO=2,OF=1,FD=2,则的值为( )BEEC组卷:835引用:8难度:0.7 -
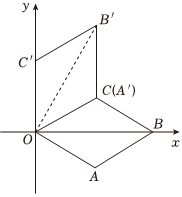 4.如图,在平面直角坐标系中,菱形OABC的边长为2,点B在x轴的正半轴上,且∠AOC=60°,将菱形OABC绕原点O逆时针方向旋转60°,得到四边形OA′B′C′(点A′与点C重合),则点B′的坐标是( )6组卷:2026引用:16难度:0.5
4.如图,在平面直角坐标系中,菱形OABC的边长为2,点B在x轴的正半轴上,且∠AOC=60°,将菱形OABC绕原点O逆时针方向旋转60°,得到四边形OA′B′C′(点A′与点C重合),则点B′的坐标是( )6组卷:2026引用:16难度:0.5 -
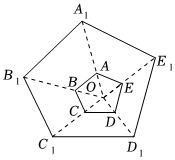 5.如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=3:4,则五边形ABCDE和五边形A1B1C1D1E1的面积比是( )组卷:70引用:1难度:0.6
5.如图,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA:OA1=3:4,则五边形ABCDE和五边形A1B1C1D1E1的面积比是( )组卷:70引用:1难度:0.6 -
6.某小组做“当试验次数很大时,用频率估计概率”的试验时,统计了某一结果出现的频率,表格如下,则符合这一结果的试验最有可能是( )
次数 100 200 300 400 500 600 700 800 900 1000 频率 0.60 0.30 0.50 0.36 0.42 0.38 0.41 0.39 0.40 0.40 组卷:969引用:9难度:0.7 -
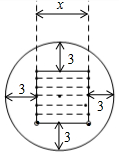 7.我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是( )组卷:502引用:19难度:0.6
7.我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是( )组卷:502引用:19难度:0.6 -
8.在△ACB中,∠ABC=90°,用直尺和圆规在AC上确定点D,使△BAD∽△CBD,根据作图痕迹判断,正确的是( )
组卷:2200引用:34难度:0.5
七、解答题(本题12分)
-
24.(1)如图1.在Rt△ACB中,∠ACB=90°,CA=8,BC=6,点D、E分别在边CA,CB上,且CD=3,CE=4,连接AE,BD,F为AE的中点,连接CF交BD于点G,则线段CG所在直线与线段BD所在直线的位置关系是.(提示:延长CF到点M,使FM=CF,连接AM)
(2)将△DCE绕点C逆时针旋转至图2所示位置时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
(3)将△DCE绕点C逆时针在平面内旋转,在旋转过程中,当B,D,E三点在同一条直线上时,CF的长为.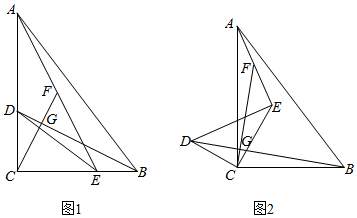 组卷:822引用:4难度:0.1
组卷:822引用:4难度:0.1
八、解答题(本题12分)
-
25.如图,在平面直角坐标系中,直线AB交x轴于点A(-2,0),交y轴于点B(0,4),直线y=kx+b经过点B且交x轴正半轴于点C,已知△ABC面积为10.
(1)点C的坐标是( ,),直线BC的表达式是 ;
(2)如图1,点E为线段AB中点,点D为y轴上一动点,连接DE,以DE为直角边作等腰直角三角形△EDF,且DE=DF,在点的运动过程中,当点F落在直线BC上时,求点D的坐标;
(3)如图2,若G为线段BC上一点,且满足S△ABG=S△ABO,点M为直线AG上一动点,在x轴上是否存在点N,使以点B,C,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.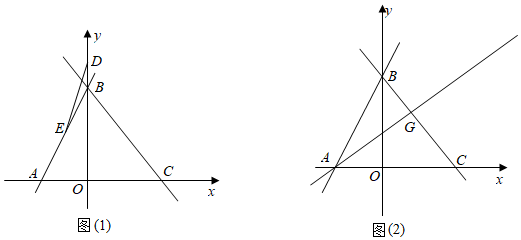 组卷:3012引用:4难度:0.3
组卷:3012引用:4难度:0.3


