2022-2023学年云南省昆明一中高二(下)期中数学试卷
发布:2024/5/17 8:0:8
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知集合A={x∈N||x|<3},B={x|-2<x≤1},则A∩B=( )
组卷:221引用:9难度:0.7 -
2.复数z满足
(i是虚数单位),则z的共轭复数z=2-ii+3i对应的点在复平面内位于( )z组卷:121引用:4难度:0.8 -
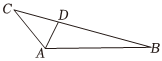 3.如图,在△ABC中,AB=6,AC=3,∠BAC=,2π3=2BD,则DC•AB=( )AD组卷:122引用:6难度:0.7
3.如图,在△ABC中,AB=6,AC=3,∠BAC=,2π3=2BD,则DC•AB=( )AD组卷:122引用:6难度:0.7 -
4.函数
的图像大致为( )f(x)=ex-1ex+1sin(π2-x)组卷:144引用:4难度:0.7 -
5.某学校共1000人参加数学测验,考试成绩ξ近似服从正态分布N(100,σ2),若P(80≤ξ≤100)=0.45,则估计成绩在120分以上的学生人数为( )
组卷:257引用:6难度:0.5 -
6.已知双曲线
,抛物线E:y2=4x的焦点为F,抛物线E的准线与双曲线C的两条渐近线分别交于点A,B,若△ABF为正三角形,则双曲线C的渐近线方程为( )C:x2a2-y2b2=1(a>0,b>0)组卷:702引用:7难度:0.7 -
7.某项活动安排了4个节目,每位观众都有6张相同的票,活动结束后将票全部投给喜欢的节目,一位观众最喜欢节目A,准备给该节目至少投3张,剩下的票则随机投给其余的节目,但必须要A节目的得票数是最多的,则4个节目获得该观众的票数情况有( )种
组卷:285引用:4难度:0.8
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知函数f(x)=ex-ln(2x+a).
(1)当0<a<2时,讨论导函数f'(x)的零点个数;
(2)当a=1时,证明:.f(x)>32-ln2组卷:39引用:1难度:0.3 -
22.已知椭圆C:
的离心率为x2a2+y2b2=1(a>b>0),其左、右焦点分别为F1、F2,上顶点为P,且32.PF1•PF2=-2
(1)求椭圆C的方程;
(2)直线l:y=kx+m(m>0)与椭圆C交于A,B两点,O为坐标原点.试求当k为何值时,|OA|2+|OB|2恒为定值,并求此时△AOB面积的最大值.组卷:172引用:5难度:0.3


