2023年北京市石景山区中考数学二模试卷

一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个.

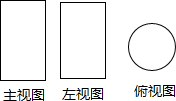• 1．某几何体的三视图如图，则该几何体是（　　）

  A．圆柱

  B．圆锥

  C．长方体

  D．三棱柱
  组卷：245引用：13难度：0.9

  解析

• 2．实数a,b在数轴上的对应点的位置如图所示，下列结论中正确的是（　　）
  

  A．a＞b

  B．|a|＞b

  C．a+b＞0

  D．a＜-3
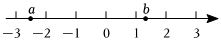  组卷：92引用：3难度：0.7

  解析

• 3．若一个多边形的内角和为540°，则该多边形的边数为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：521引用：6难度：0.5

  解析

• 4．如图，在△ABC中，M，N分别是边AB，AC上的点，MN∥BC，BM=2AM．若△AMN的面积为1，则△ABC的面积为（　　）

  A．2

  B．3

  C．4

  D．9
  组卷：310引用：6难度：0.5

  解析

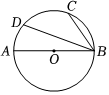• 5．如图，AB为⊙O的直径，C，D为⊙O上的点，

  ˆ

  BC

  =

  ˆ

  DC

  ．若∠CBD=35°，则∠ABD的度数为（　　）

  A．20°

  B．35°

  C．40°

  D．70°
  组卷：1119引用：9难度：0.8

  解析

• 6．一组数据：1，2，5，0，2，若添加一个数据2，则发生变化的统计量是（　　）

  A．平均数

  B．中位数

  C．众数

  D．方差
  组卷：313引用：4难度：0.7

  解析

• 7．如图显示了某林业部门统计某种树苗在本地区相同条件下的移植成活试验的结果．
  
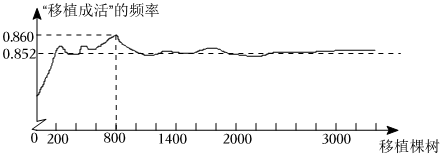
  下面有四个推断：
  ①当移植的棵数是800时，成活的棵数是688，所以“移植成活”的概率是0.860；
  ②随着移植棵数的增加，“移植成活”的频率总在0.852附近摆动，显示出一定的稳定性，可以估计“移植成活”的概率是0.852；
  ③与试验相同条件下，若移植10000棵这种树苗，可能成活8520棵；
  ④在用频率估计概率时，移植3000棵树时的频率0.852一定比移植2000棵树时的频率0.853更准确
  其中合理的是（　　）

  A．①②

  B．①③

  C．②③

  D．②④
  组卷：303引用：4难度：0.5

  解析

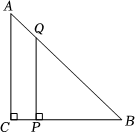• 8．如图，在Rt△ACB中，∠ACB=90°，CA=CB=10．点P是CB边上一动点（不与点C，B重合），过点P作PQ⊥CB交AB于点Q．设CP=x,BQ的长为y,△BPQ的面积为S，则y与x,S与x满足的函数关系分别为（　　）

  A．一次函数关系，二次函数关系

  B．反比例函数关系，二次函数关系

  C．一次函数关系，反比例函数关系

  D．反比例函数关系，一次函数关系
  组卷：503引用：4难度：0.6

  解析

二、填空题（共16分，每题2分）

• 9．若

  x

  -

  3

  在实数范围内有意义，则实数x的取值范围为

  ．
  组卷：1092引用：69难度：0.7

  解析

三、解答题（共68分，第17-20题，每题5分，第21题6分，第22-23题，每题5分，第24-26题，每题6分，第27-28题，每题7分）解答应写出文字说明、演算步骤或证明过程.

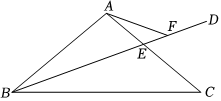• 27．如图，在△ABC中，AB=AC，∠ACB=2α，BD平分∠ABC交AC于点E，点F是ED上一点且∠EAF=α，
  （1）求∠AFB的大小（用含α的式子表示）；
  （2）连接FC．用等式表示线段FC与FA的数量关系，并证明．
  组卷：701引用：2难度：0.5

  解析

• 28．在平面直角坐标系xOy中，对于点M（不与点O重合）和线段PQ，给出如下定义：连接OM，平移线段OM，使点M与线段PQ的中点M′重合，得到线段O′M”，则称点O′为线段PQ的“中移点”．已知⊙O的半径为1．
  （1）如图，点P（-1，0），点Q（m,4），
  ①点M为⊙O与y轴正半轴的交点，

  OO

  ′

  =

  5

  ，求m的值；
  ②点M为⊙O上一点，若在直线y=x+3上存在线段PQ的“中移点”O′，求m的取值范围．
  （2）点Q是⊙O上一点，点M在线段OQ上，且OM=t（0

  ＜

  t

  ＜

  1

  2

  ）．若P是⊙O外一点，点O′为线段PQ的“中移点”，连接OO′，当点Q在⊙O上运动时，直接写出OO′长的最大值与最小值的差（用含t的式子表示）．
  
  组卷：565引用：4难度：0.5

  解析