2022-2023学年江苏省盐城市射阳中学高一（上）入学数学试卷

一、单选题。本大题共8小题，每小题5分，共计40分。每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．计算（-xy²）³的结果是（　　）

  A．-x3y6

  B．x3y6

  C．x4y5

  D．-x4y5
  组卷：35引用：2难度：0.7

  解析

• 2．下列各组对象中能构成集合的是（　　）

  A．充分接近 3 的实数的全体

  B．数学成绩比较好的同学

  C．小于20的所有自然数

  D．未来世界的高科技产品
  组卷：276引用：4难度：0.9

  解析

• 3．三角形的重心是三角形的（　　）

  A．三条中线的交点

  B．三条角平分线的交点

  C．三条高所在直线的交点

  D．三条边的垂直平分线的交点
  组卷：7引用：2难度：0.8

  解析

• 4．某篮球兴趣小组7名学生参加投篮比赛，每人投10个，投中的个数分别为：8、5、7、5、8、6、8，则这组数据的众数和中位数分别为（　　）

  A．5、7

  B．6、7

  C．8、5

  D．8、7
  组卷：96引用：6难度：0.8

  解析

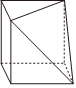• 5．过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥所得到的几何体如图所示，它的左视图是（　　）

  A．

  B．

  C．

  D．
  组卷：20引用：3难度：0.9

  解析

• 6．二次函数y=x²+2x-m²+1的图像与直线y=1的公共点个数是（　　）

  A．0

  B．1

  C．2

  D．1或2
  组卷：18引用：2难度：0.7

  解析

• 7．“x＞1且y＞2“是“x+y＞3“的 （　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：53引用：5难度：0.8

  解析

四、解答题。（解答题要有必要的文字说明和推理过程，仅有答案不给分）

• 21．已知点P（x₀，y₀）和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=

  |

  k

  x

  0

  -

  y

  0

  +

  b

  |

  1

  +

  k

  2

  计算．
  例如：求点P（-1，2）到直线y=3x+7的距离．
  解：Q直线y=3x+7，其中k=3，b=7．
  ∴点P（-1，2）到直线y=3x+7的距离为：d=

  |

  k

  x

  0

  -

  y

  0

  +

  b

  |

  1

  +

  k

  2

  =

  |

  3

  ×

  （

  -

  1

  ）

  -

  2

  +

  7

  |

  1

  +

  3

  2

  =

  2

  10

  =

  10

  5

  ．
  根据以上材料，解答下列问题：
  （1）求点P（-1，3）到直线y=x-3的距离；
  （2）已知⊙Q的圆心Q坐标为（0，3），半径r为3，判断⊙Q与直线y=

  3

  x+9的位置关系，并说明理由；
  （3）已知直线y=3x+3与y=3x-6平行，求这两条直线之间的距离．
  组卷：26引用：2难度：0.7

  解析

• 22．如图，抛物线y=

  2

  m

  x²-2x与x轴的负半轴交于点A，对称轴经过顶点B与x轴交于点M．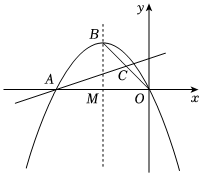
  （1）求抛物线的顶点B的坐标（用含m的代数式表示）；
  （2）连结BO，若BO的中点C的坐标为（-

  3

  2

  ，

  3

  2

  ），求抛物线的解析式；
  （3）在（2）的条件下，D在抛物线上，E在直线BM上，若以A、C、D、E为顶点的四边形是平行四边形，求点D的坐标．
  组卷：7引用：3难度：0.5

  解析