当前位置：试卷中心 > 试卷详情

2022-2023学年广东省佛山市顺德区八年级（上）第一次学业评价数学试卷

发布：2024/9/14 10:0:8

一、单选题（每小题3分，共30分）

1．下列各实数中，属于无理数的是（　　）
A．
1
3
B．3.14 C．0 D．
5
组卷：33引用：3难度：0.7
解析
2．下列每一组数据中的三个数值分别为三角形的三边长，不能构成直角三角形的是（　　）
A．3、4、5 B．6、8、10 C．
3
、2、
5
D．5、12、13
组卷：1212引用：84难度：0.9
解析
3．下列各式计算正确的是（　　）
A．
2
+
3
=
5
B．4
3
-3
3
=1 C．
27
÷
3
=3 D．2
3
×3
3
=6
组卷：718引用：21难度：0.9
解析
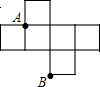4．如图是边长为1的六个小正方形组成的平面图形，经过折叠能围成一个正方体，那么点A、B在围成的正方体上相距（　　）
A．0 B．1 C．
2
D．
3
组卷：300引用：4难度：0.9
解析
5．下列说法中，不正确的是（　　）
A．10的立方根是
3
10
B．
4
9
的平方根是
2
3
C．-2是4的一个平方根
D．0.01的算术平方根是0.1
组卷：565引用：28难度：0.9
解析
6．等边三角形的边长为2，则它的面积为（　　）
A．
3
B．
2
3
C．
2
5
D．
2
6
组卷：193引用：3难度：0.5
解析
7．若实数m、n满足|m-2|+
n
-
4
=0，且m、n恰好是等腰△ABC的两条边的边长，则△ABC的周长是（　　）
A．12 B．10 C．8 D．10或8
组卷：627引用：13难度：0.6
解析
8．估算
26
+
1
的值（　　）
A．在3与4之间 B．在4与5之间 C．在5与6之间 D．在6与7之间
组卷：189引用：3难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

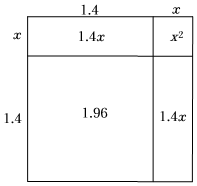24．“说不完的
2
”探究活动，根据各探究小组的汇报，完成下列问题．
（1）
2
到底有多大？
下面是小欣探索
2
的近似值的过程，请补充完整：
我们知道面积是2的正方形边长是
2
，且
2
＞
1
.
4
．设
2
=
1
.
4
+
x
，画出如下示意图．
由面积公式，可得x²+
=2．
因为x值很小，所以x²更小，略去x²，
得方程
，
解得x≈
（保留到0.001），
即
2
≈

．
（2）怎样画出
2
？请一起参与小敏探索画
2
过程．
现有2个边长为1的正方形，排列形式如图（1），请把它们分割后拼接成一个新的正方形．要求：画出分割线并在正方形网格图（图中每个小正方形的边长均为1）中用实线画出拼接成的新正方形．
小敏同学的做法是：设新正方形的边长为x（x＞0）．依题意，割补前后图形的面积相等，有x²=2，解得
x
=
2
．把图（1）如图所示进行分割，请在图（2）中用实线画出拼接成的新正方形．

请参考小敏做法，现有5个边长为1的正方形，排列形式如图（3），请把它们分割后拼接成一个新的正方形．要求：画出分割线并在正方形网格图（4）中用实线画出拼接成的新正方形．说明：直接画出图形，不要求写分析过程．
组卷：401引用：6难度：0.5
解析
25．阅读理解：在平面直角坐标系中，P₁（x₁，y₁），P₂（x₂，y₂），如何求P₁P₂的距离．
如图1，在Rt△P₁P₂Q中，|P₁P₂|²=|P₁Q|²+|P₂Q|²=（x₂-x₁）²+（y₂-y₁）²，所以
|P₁P₂|=
（
x
2
-
x
1
）
2
+
（
y
2
-
y
1
）
2
．因此，我们得到平面上两点P₁（x₁，y₁），P₂（x₂，y₂）之间
的距离公式为|P₁P₂|=
（
x
2
-
x
1
）
2
+
（
y
2
-
y
1
）
2
．根据上面得到的公式，解决下列问题：
（1）若已知平面两点A（1，6），B（4，10），则AB的距离为
；
（2）若平面内三点A（-5，3），B（2，4），C（1，1），请运用给出的公式，试判断△ABC的形状，并说明理由；
（3）如图2，在正方形AOBC中，A（-4，3），点D在OA边上，且D（-2，
3
2
），直线l经过O，C两点，点E是直线l上的一个动点，请直接写出DE+EA的最小值．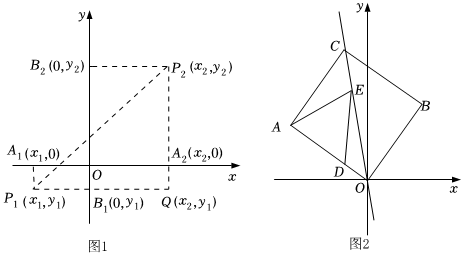
组卷：459引用：2难度：0.5
解析