2022-2023学年辽宁省沈阳市郊联体高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是得合题目要求的.

• 1．已知复数z满足z-iz=2，则|z|=（　　）

  A． 2

  B． 5

  C．2

  D．5
  组卷：80引用：8难度：0.7

  解析

• 2．已知角α的终边经过点P（1，m）（m＜0），则下列各式一定为正的是（　　）

  A．sinα

  B．tanα

  C．cosα

  D． cosα tanα
  组卷：122引用：5难度：0.7

  解析

• 3．△ABC中角A，B，C所对的边分别是a,b,c,若a²+b²-c²=

  3

  ab,则角C为（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  组卷：251引用：5难度：0.9

  解析

• 4．cos165°=（　　）

  A． 2 - 6 4

  B． 6 + 2 4

  C． 6 - 2 4

  D． - 6 + 2 4
  组卷：123引用：6难度：0.7

  解析

• 5．已知向量

  a

  =

  （

  2

  ，-

  1

  ）

  ，

  b

  =

  （

  1

  ，

  n

  ）

  ，若

  a

  ⊥

  b

  ，则

  a

  +

  b

  在

  b

  上的投影向量的坐标为（　　）

  A．（2，1）

  B．（1，1）

  C．（1，2）

  D．（-2，1）
  组卷：180引用：9难度：0.7

  解析

• 6．已知m,n是两条不同直线，α，β，γ是三个不同的平面，则下列命题中正确的是（　　）

  A．若m⊥α，n⊥α，则m∥n

  B．若α⊥β，β⊥γ，则α⊥γ

  C．若m∥α，α⊥β，则m⊥β

  D．若m,n是异面直线，且m⊂α，n⊂β，m∥β，则n∥α
  组卷：64引用：3难度：0.7

  解析

• 7．一艘海轮从A处出发，以每小时40海里的速度沿南偏东40°的方向直线航行，2小时后到达B处，在C处有一座灯塔，海轮在A处观察灯塔，其方向是南偏东70°，在B处观察灯塔，其方向是北偏东65°，那么B，C两点间的距离是（　　）

  A． 40 2 海里

  B． 40 3 海里

  C． 80 3 海里

  D． 80 2 海里
  组卷：313引用：11难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知向量

  a

  =

  （

  cosx

  ,

  sinx

  ）

  ，

  b

  =

  （

  3

  cosx

  ,

  2

  cosx

  -

  3

  sinx

  ）

  ，设函数

  f

  （

  x

  ）

  =

  a

  •

  b

  ．
  （1）求f（x）的单调递减区间；
  （2）若函数

  g

  （

  x

  ）

  =

  f

  （

  x

  -

  π

  6

  ）

  +

  af

  （

  x

  2

  -

  π

  6

  ）

  -

  af

  （

  x

  2

  +

  π

  12

  ）

  在区间[0，π]上的最大值为6，求实数a的值．
  组卷：177引用：5难度：0.6

  解析

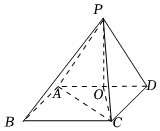• 22．如图，已知四棱锥P-ABCD的底面为矩形，AB=PD=2，

  AD

  =

  2

  2

  ，O是AD的中点，PO⊥平面ABCD．
  （1）求证：AC⊥平面POB；
  （2）设平面PAB与平面PCD的交线为l.
  （i）求证：l∥AB；
  （ii）求l与平面PAC所成角的大小．
  组卷：158引用：8难度：0.6

  解析