当前位置：试卷中心 > 试卷详情

2022-2023学年山东省德州市高二（下）期末数学试卷

发布：2024/6/28 8:0:9

一、选择题（本题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合要求的.）

1．若集合M={x|log₂x＜-1}，
N
=
{
x
|
3
x
≥
1
3
}
，则M∩N=（　　）
A．
{
x
|
-
1
≤
x
＜
1
2
}
B．
{
x
|
-
1
＜
x
＜
1
2
}
C．
{
x
|
0
≤
x
＜
1
2
}
D．
{
x
|
0
＜
x
＜
1
2
}
组卷：36引用：3难度：0.9
解析
2．设函数f（x）=
1
+
lo
g
2
（
2
-
x
）
，
x
＜
1
2
x
，
x
≥
1
，则f（-2）+f（log₂6）=（　　）
A．3 B．6 C．9 D．12
组卷：70引用：5难度：0.9
解析
3．设a∈R，则“a=1”是“
f
（
x
）
=
ln
（
x
2
+
1
+
ax
）
为奇函数”的（　　）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
组卷：288引用：8难度：0.6
解析
4．设a=e^0.7，b=3^0.8，c=log₃e,则a,b,c的大小关系为（　　）
A．a＜b＜c B．c＜b＜a C．c＜a＜b D．b＜c＜a
组卷：48引用：2难度：0.7
解析
5．如果等比数列{a_n}的前n项和S_n=2ⁿ⁺¹+a,则常数a=（　　）
A．-1 B．1 C．-2 D．2
组卷：730引用：2难度：0.8
解析
6．定义在R上的偶函数f（x）满足f（-x+2）=f（x+2），且
f
（
1
）
=
1
3
，则f（2023）的值为（　　）
A．-2 B．-1 C．
-
1
3
D．
1
3
组卷：183引用：3难度：0.8
解析
7．随着国家对中小学“双减”政策的逐步落实，其中增加中学生体育锻炼时间的政策引发社会的广泛关注．某教育时报为研究“支持增加中学生体育锻炼时间的政策是否与性别有关”，从某校男女生中各随机抽取80名学生进行问卷调查，得到如表数据（10≤m≤20，m∈N^*）

支持不支持

男生 70-m 10+m

女生 50+m 30-m

通过计算有95%以上的把握认为“支持增加中学生体育锻炼时间的政策与性别有关”，则在这被调查的80名女生中支持增加中学生体育锻炼时间的人数的最小值为（　　）
附：
K
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，其中n=a+b+c+d.

P（K²≥k₀） 0.100 0.050 0.010 0.005 0.001

k₀ 2.706 3.841 6.635 7.879 10.828

A．15 B．65 C．16 D．66
组卷：54引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本题共6小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤.）

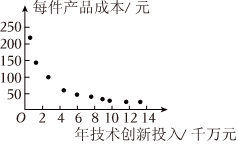21．2020年11月，国务院办公厅印发《新能源汽车产业发展规划（2021-2035年）》，要求深入实施发展新能源汽车国家战略，推动中国新能源汽车产业高质量可持续发展，加快建设汽车强国．同时为了推广新能源替代传统非绿色能源，除了财政补贴、税收优惠等激励性政策外，可间接通过前期技术研发支持等政策引导能源发展方向．某企业多年前就开始进行新能源汽车方面的研发，现对近10年的年技术创新投入x_i和每件产品成本y_i（i=1，2，3，…，10）的数据进行分析，得到如下散点图，并计算得：
x
=
6
.
8
，
y
=
70
，
10
∑
i
=
1
1
x
i
=
3
，
10
∑
i
=
1
1
x
2
i
=
1
.
6
，
10
∑
i
=
1
y
i
x
i
=
350
．
（1）根据散点图可知，可用函数模型
y
=
b
x
+
a
拟合y与x的关系，试建立y关于x的回归方程；
（2）已知该产品的年销售额m（单位：千万元）与每件产品成本y的关系为
m
=
-
y
2
300
+
y
10
+
200
y
-
10
+
100
．该企业的年投入成本除了年技术创新投入，还要投入其他成本10千万元，根据（1）的结果回答：当年技术创新投入x为何值时，年利润的预报值最大？（注：年利润=年销售额-年投入成本）
参考公式：对于一组数据（u₁，v₁），（u₂，v₂），…，（u_n，v_n），其回归直线v=α+βu的斜率和截距的最小二乘估计分别为：
̂
β
=
n
∑
i
=
1
u
i
v
i
-
n
u
v
n
∑
i
=
1
u
2
i
-
n
u
2
，
̂
α
=
v
-
̂
β
u
．
组卷：24引用：3难度：0.5
解析
22．已知函数
f
（
x
）
=
alnx
-
1
x
-
2
x
，a∈R．
（1）当a=1时，判断f（x）的零点个数；
（2）若
f
（
x
）
+
e
x
+
1
x
+
2
x
≥
e
恒成立，求实数a的值．
组卷：28引用：2难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．充分不必要条件	B．必要不充分条件
C．充要条件	D．既不充分也不必要条件

P（K²≥k₀）	0.100	0.050	0.010	0.005	0.001
k₀	2.706	3.841	6.635	7.879	10.828

	支持	不支持
男生	70-m	10+m
女生	50+m	30-m

2022-2023学年山东省德州市高二（下）期末数学试卷

一、选择题（本题共8个小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合要求的.）

1．若集合M={x|log2x＜-1}，N={x|3x≥13}，则M∩N=（ ）

2．设函数f（x）=1+log2（2-x），x＜12x，x≥1，则f（-2）+f（log26）=（ ）

3．设a∈R，则“a=1”是“f（x）=ln（x2+1+ax）为奇函数”的（ ）

4．设a=e0.7，b=30.8，c=log3e,则a,b,c的大小关系为（ ）

5．如果等比数列{an}的前n项和Sn=2n+1+a,则常数a=（ ）

6．定义在R上的偶函数f（x）满足f（-x+2）=f（x+2），且f（1）=13，则f（2023）的值为（ ）

四、解答题（本题共6小题，共70分，解答应写出必要的文字说明、证明过程或演算步骤.）

22．已知函数f（x）=alnx-1x-2x，a∈R．（1）当a=1时，判断f（x）的零点个数；（2）若f（x）+ex+1x+2x≥e恒成立，求实数a的值．

1．若集合M={x|log₂x＜-1}，
N
=
{
x
|
3
x
≥
1
3
}
，则M∩N=（　　）

2．设函数f（x）=
1
+
lo
g
2
（
2
-
x
）
，
x
＜
1
2
x
，
x
≥
1
，则f（-2）+f（log₂6）=（　　）

3．设a∈R，则“a=1”是“
f
（
x
）
=
ln
（
x
2
+
1
+
ax
）
为奇函数”的（　　）

4．设a=e^0.7，b=3^0.8，c=log₃e,则a,b,c的大小关系为（　　）

5．如果等比数列{a_n}的前n项和S_n=2ⁿ⁺¹+a,则常数a=（　　）

6．定义在R上的偶函数f（x）满足f（-x+2）=f（x+2），且
f
（
1
）
=
1
3
，则f（2023）的值为（　　）

22．已知函数
f
（
x
）
=
alnx
-
1
x
-
2
x
，a∈R．
（1）当a=1时，判断f（x）的零点个数；
（2）若
f
（
x
）
+
e
x
+
1
x
+
2
x
≥
e
恒成立，求实数a的值．