2022-2023学年江苏省常州市武进区高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若复数z是x²+x+2=0的根，则|z|=（　　）

  A．1

  B． 2

  C．2

  D．3
  组卷：55引用：5难度：0.8

  解析

• 2．一个三角形的三条高的长度分别是

  1

  6

  ，

  1

  10

  ，

  1

  14

  ，则该三角形（　　）

  A．一定是锐角三角形

  B．一定是直角三角形

  C．一定是钝角三角形

  D．有可能是锐角三角形，也可能是钝角三角形
  组卷：33引用：4难度：0.8

  解析

• 3．已知l,m,n表示不同的直线，α，β，γ表示不同的平面，则下列四个命题正确的是（　　）

  A．若l∥α，且m∥α，则l⊥m	B．若α⊥β，m∥α，n⊥β，则m∥n
  C．若m∥l,且m⊥α，则l⊥α	D．若m⊥n,m⊥α，n∥β，则α⊥β
  组卷：69引用：4难度：0.5

  解析

• 4．已知

  cos

  （

  α

  -

  π

  6

  ）

  =

  1

  3

  ，则

  sin

  （

  2

  α

  +

  π

  6

  ）

  =（　　）

  A． - 7 9

  B． 7 9

  C． - 2 2 3

  D． 2 2 3
  组卷：404引用：10难度：0.7

  解析

• 5．疫情期间，一同学通过网络平台听网课，在家坚持学习．某天上午安排了四节网课，分别是数学，语文，政治，地理，下午安排了三节，分别是英语，历史，体育．现在，他准备在上午下午的课程中各任选一节进行打卡，则选中的两节课中至少有一节文综学科（政治、历史、地理）课程的概率为（　　）

  A． 3 4

  B． 7 12

  C． 2 3

  D． 5 6
  组卷：205引用：7难度：0.7

  解析

• 6．已知z₁，z₂∈C，|z₁|=|z₂|=1，|z₁+z₂|=

  3

  ，则|z₁-z₂|=（　　）

  A．1

  B． 2

  C． 3

  D．2
  组卷：117引用：5难度：0.7

  解析

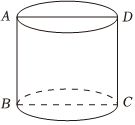• 7．如图，某圆柱体的高为2，ABCD是该圆柱体的轴截面．已知从点B出发沿着圆柱体的侧面到点D的路径中，最短路径的长度为

  2

  5

  ，则该圆柱体的体积是（　　）

  A．3

  B． 4 π

  C．32π

  D． 32 π
  组卷：93引用：3难度：0.8

  解析

四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.

• 21．甲、乙、丙三个学校进行篮球比赛，各出一个代表队，简称甲队、乙队、丙队．约定赛制如下：累计负两场者被淘汰；比赛前抽签决定首先比赛的两个队，另一队轮空；每场比赛的胜队与轮空队进行下一场比赛，负队下一场轮空，直至有一队被淘汰；当一队被淘汰后，剩余的两队继续比赛，直至其中一队被淘汰，另一队最终获胜，比赛结束．已知在每场比赛中，甲队胜乙队和甲队胜丙队的概率均为

  2

  3

  ，乙队胜丙队的概率为

  1

  2

  ，各场比赛的结果相互独立．经抽签，第一场比赛甲队轮空．
  （1）求“前三场比赛结束后，乙队被淘汰”的概率；
  （2）求“一共只需四场比赛甲队就获得冠军”的概率；
  （3）求“需要进行第五场比赛”的概率．
  组卷：179引用：3难度：0.7

  解析

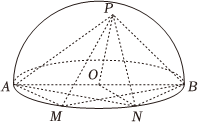• 22．如图，AB是半球的直径，O为球心，AB=4，M，N依次是半圆上的两个三等分点，P是半球面上一点，且PN⊥MB．
  （1）证明：平面PBM⊥平面PON；
  （2）若点P在底面圆内的射影恰在BM上，求点M到平面PAB的距离．
  组卷：86引用：3难度：0.4

  解析