2022-2023学年福建省莆田五中高一(上)暑期返校数学试卷(一)
发布:2024/8/7 8:0:9
一、单选题
-
1.i为虚数单位,复数z满足z(2-i)=i2022,则下列说法正确的是( )
组卷:103引用:4难度:0.8 -
2.设α,β满足
,tan(α+3π4)=3,则tan(α+β)=( )tan(β+π4)=2组卷:319引用:3难度:0.6 -
3.某科考试成绩公布后,发现判错一道题,经修改后重新公布,如表是抽取10名学生的成绩,依据这些信息修改后的成绩与修改前的相比,这10名学生成绩的( )
学生学号 1 2 3 4 5 6 7 8 9 10 修改前成绩 126 130 104 100 133 123 100 120 139 103 修改后成绩 126 135 99 100 138 123 95 120 144 98 组卷:134引用:3难度:0.7 -
4.已知m,n是两条不同的直线,α,β是两个不同的平面,则下列判断正确的是( )
组卷:52引用:2难度:0.6 -
5.若向量
,a满足|b|=|a|=2,b,则|a+b|=23在a-b上的投影向量为( )b组卷:8引用:1难度:0.8 -
6.锐角△ABC的三个内角A,B,C所对的边分别是a,b,c,某数学兴趣小组探究该三角形时,提出以下四个论断:甲:B>C;乙:cosB<cosC;丙:cosB<sinC;丁:ccosB<bcosC.若上述四个论断中有且只有一个是正确的,则正确的是( )
组卷:43引用:3难度:0.7 -
7.如图是北京2022年冬奥会会徽的图案,奥运五环的大小和间距如图所示.若圆半径均为12,相邻圆圆心水平路离为26,两排圆圆心垂直距离为11.设五个圆的圆心分别为O1、O2、O3、O4、O5,则
的值为( )O4O1•(O4O5+O4O2)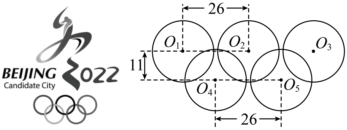 组卷:83引用:4难度:0.8
组卷:83引用:4难度:0.8
四、解答题
-
22.在平面四边形ABCD中,点B,D在直线AC的两侧,AB=3,BC=5,四个内角分别用A,B,C,D表示,cosB=-cosD=
.35
(1)求∠BAC;
(2)求△ABD与△ACD的面积之和的最大值.组卷:108引用:5难度:0.5 -
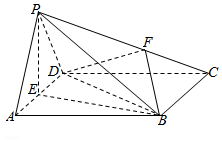 23.如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,△PAD是正三角形,E为线段AD的中点,.PF=λFC(λ>0)
23.如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,△PAD是正三角形,E为线段AD的中点,.PF=λFC(λ>0)
(1)求证:平面PBC⊥平面PBE;
(2)是否存在点F,使得?若存在,求出λ的值;若不存在,请说明理由.VB-PAE=58VD-PFB
(3)若平面PAD⊥平面ABCD,在平面PBE内确定一点H,使CH+FH的值最小,并求此时的值.BHBP组卷:537引用:3难度:0.3


