2023-2024学年广东省梅州市大埔县虎山中学高三（上）开学数学试卷（8月份）
发布：2024/8/6 8:0:9
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
-
1．设全集U={-3，-2，-1，0，1，2，3}，集合A={-1，0，1，2}，B={-3，2，3}，则A∩（∁UB）=（ ）
组卷：501引用：5难度：0.8 -
2．已知sin（α+
）=π3，则sin（2α+223）的值为（ ）π6组卷：621引用：5难度：0.7 -
3．某种活性细胞的存活率y（%）与存放温度x（℃）之间具有线性相关关系，样本数据如表所示：
经计算，回归直线的斜率为-3.2．若这种活性细胞的存放温度为6℃，则其存活率的预报值为（ ）存放温度x（℃） 10 4 -2 -8 存活率y（%） 20 44 56 80 组卷：46引用：2难度：0.8 -
4．已知函数
，则f（log212）=（ ）f（x）=（12）x，x≤2f（x-1），x＞2组卷：65引用：3难度：0.7 -
5．已知a＞0，则“a＞2”是“aa＞a2”的（ ）
组卷：88引用：3难度：0.7 -
6．已知f（x）=x-sinx,则不等式f（2m+1）+f（1-m）＞0的解集为（ ）
组卷：256引用：7难度：0.7 -
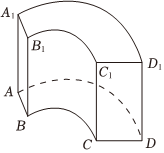7．中国古代数学瑰宝《九章算术》中记载了一种称为“曲池”的几何体，该几何体为上、下底面均为扇环形的柱体（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池，其中AA1⊥底面ABCD，底面扇环所对的圆心角为，π2的长度为ˆAD的长度的3倍，AA1=3，CD=2，则该曲池的体积为（ ）ˆBC组卷：57引用：2难度：0.7
四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
-
21．某社区消费者协会为了解本社区居民网购消费情况，随机抽取了100位居民作为样本，就最近一年来网购消费金额，网购次数和支付方式等进行了问卷调查．经统计，这100位居民的网购消费金额均在区间[0，30]内（单位：千元），按[0，5），（5，10]，（10，15]，（15，20]，（20，25]，[25，30]分成6组，其频率分布直方图如图．
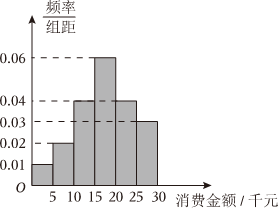
（1）将一年来网购消费金额在20千元以上称为“网购迷”，补全下面的2×2列联表，并判断有多大把握认为“网购迷与性别有关系”；
（2）估计该社区居民最近一年来网购消费金额的中位数；男 女 合计 网购迷 20 非网购迷 45 合计 100
（3）调查显示，甲、乙两人每次网购采用的支付方式相互独立，两人网购时间与次数也互不影响．统计最近一年来两人网购的总次数与支付方式，所得数据如下表所示：
将频率视为概率，若甲、乙两人在下周内各自网购2次，记两人采用支付宝支付的次数之和为ξ，求ξ的数学期望．网购总次数 支付宝支付次数 银行卡支付次数 微信支付次数 甲 80 40 16 24 乙 90 60 18 12
附：观测值公式：．临界值表：K2=（a+b+c+d）（ad-bc）2（a+b）（c+d）（a+c）（b+d）P（K2≥k0） 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.706 3.841 5.024 6.635 7.879 10.828 组卷：8引用：2难度：0.5 -
22．已知函数f（x）=x3+alnx,其中a≥-3为常数．
（1）设f'（x）为f（x）的导函数，当a=6时，求函数的极值；g（x）=f（x）-f′（x）+9x
（2）设点A（x1，f（x1）），B（x2，f（x2））（x1＞x2≥1），曲线y=f（x）在点A，B处的切线的斜率分别为k1，k2，直线AB的斜率为k,证明：k1+k2＞2k.组卷：67引用：3难度：0.3
