当前位置：试卷中心 > 试卷详情

2022-2023学年甘肃省张掖市某重点校高一（下）月考数学试卷（5月份）

发布：2024/5/15 8:0:8

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

1．命题：“∀x∈R，x²-x+2≥0”的否定是（　　）
A．∀x∉R，x²-x+2≥0 B．∃x∉R，x²-x+2≥0
C．∃x∈R，x²-x+2＜0 D．∀x∈R，x²-x+2＜0
组卷：124引用：11难度：0.7
解析
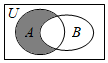2．集合U=R，A={x|x²-x-2＜0}，B={x|y=
1
1
-
x
}，则图中阴影部分所表示的集合是（　　）
A．{x|1≤x≤2} B．{x|1＜x＜2} C．{x|1≤x＜2} D．{x|1＜x≤2}
组卷：93引用：4难度：0.7
解析
3．设函数f（x）=ln（2+x）-ln（2-x），则f（x）是（　　）
A．奇函数，且在（0，2）上是增函数
B．奇函数，且在（0，2）上是减函数
C．偶函数，且在（0，2）上是增函数
D．偶函数，且在（0，2）上是减函数
组卷：261引用：4难度：0.5
解析
4．在△ABC中，B=
π
4
，BC边上的高等于
1
3
BC，则cosA等于（　　）
A．
3
10
10
B．
10
10
C．-
10
10
D．-
3
10
10
组卷：8001引用：68难度：0.7
解析
5．Logistic模型是常用数学模型之一，可应用于流行病学领域．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I（t）（t的单位：天）的Logistic模型：I（t）=
K
1
+
e
-
0
.
23
（
t
-
53
）
，其中K为最大确诊病例数．当I（t^*）=0.95K时，标志着已初步遏制疫情，则t^*约为（　　）（ln19≈3）
A．60 B．63 C．66 D．69
组卷：6565引用：62难度：0.5
解析
6．设a=log₃2，b=log₅3，c=
2
3
，则（　　）
A．a＜c＜b B．a＜b＜c C．b＜c＜a D．c＜a＜b
组卷：6232引用：24难度：0.8
解析
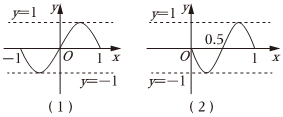7．已知函数f（x）=sinπx的图象的一部分如图（1）所示，则图（2）中的函数图象所对应的函数解析式是（　　）
A．
y
=
f
（
2
x
-
1
2
）
B．
y
=
f
（
x
2
-
1
2
）
C．
y
=
f
（
x
2
-
1
）
D．y=f（2x-1）
组卷：102引用：7难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

21．已知函数f（θ）=-sin²θ-4cosθ+4，g（θ）=m•cosθ．
（1）对任意的
θ
∈
[
0
，
π
2
]
，若f（θ）≥g（θ）恒成立，求m的取值范围；
（2）对任意的
θ
1
∈
[
0
，
π
2
]
，存在
θ
2
∈
[
0
，
π
2
]
，使得f（θ₁）=g（θ₂），求m的取值范围．
组卷：10引用：1难度：0.5
解析
22．已知函数
f
（
x
）
=
sin
（
ωx
+
π
3
）
，ω＞0；
（1）当ω=2时，求f（x）在
[
0
，
π
2
]
的值域；
（2）若至少存在三个
x
0
∈
（
0
，
π
3
）
使得f（x₀）=-1，求ω的取值范围；
（3）若f（x）在
[
π
2
，
π
]
上是增函数，且存在
m
∈
[
π
2
，
π
]
，使得
f
（
2
m
-
π
3
ω
）
＞
2
2
成立，求实数ω的取值范围．
组卷：190引用：3难度：0.6
解析