2022-2023学年天津市红桥区高二（下）期末数学试卷

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设全集U={1，2，3，4}，集合A={1，2}，B={1，3}，则（∁_UA）∩B=（　　）

  A．{1}

  B．{2}

  C．{3}

  D．{2，3，4}
  组卷：161引用：1难度：0.8

  解析

• 2．命题“∀x∈（0，+∞），总有x²+1≥2x”的否定是（　　）

  A．∀x∈（0，+∞），总有x2+1＜2x

  B．∀x∉（0，+∞），总有x2+1＜2x

  C．∃x∈（0，+∞），使得x2+1＜2x

  D．∃x∉（0，+∞），使得x2+1≥2x
  组卷：355引用：5难度：0.9

  解析

• 3．“|x-1|＜2成立”是“x（x-3）＜0成立”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：798引用：27难度：0.9

  解析

• 4．设

  a

  =

  2

  -

  1

  2

  ，

  b

  =

  （

  1

  2

  ）

  -

  2

  ，

  c

  =

  lg

  1

  2

  ，则a,b,c的大小关系为（　　）

  A．a＞b＞c

  B．b＞a＞c

  C．a＞c＞b

  D．c＞b＞a
  组卷：211引用：1难度：0.5

  解析

• 5．下列函数中，在其定义域内既是奇函数又是减函数的是（　　）

  A． y = lo g 1 2 x （ x ＞ 0 ）	B．y=-x2（x∈R）
  C．y=-x3-x（x∈R）	D． y = - 1 x （x∈R且x≠0）
  组卷：256引用：1难度：0.7

  解析

• 6．函数f（x）=

  2

  x

  -lnx的零点所在的区间为（　　）

  A．（1，2）

  B．（2，3）

  C．（3，4）

  D．（4，5）
  组卷：344引用：5难度：0.7

  解析

• 7．已知i是虚数单位，复数

  z

  =

  1

  +

  i

  i

  ，则z在复平面内对应的点的坐标在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：168引用：2难度：0.7

  解析

• 8．已知某圆柱的高为5，底面半径为

  3

  ，则该圆柱的体积为（　　）

  A．6π

  B．9π

  C．12π

  D．15π
  组卷：111引用：2难度：0.7

  解析

三、解答题：本大题共5小题，共66分.解答应写出文字说明、证明过程或演算步骤.

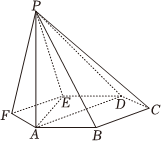• 25．如图，六棱锥P-ABCDEF的底面是边长为1的正六边形，PA⊥平面ABC，PA=2

  3

  ．
  （Ⅰ）求证：直线BC∥平面PAD；
  （Ⅱ）求证：直线ED⊥平面PAE；
  （Ⅲ）求直线PD与平面ABC所成的角．
  组卷：127引用：2难度：0.5

  解析

• 26．已知函数

  f

  （

  x

  ）

  =

  ax

  +

  1

  x

  ．
  （1）判断f（x）的奇偶性；
  （2）若a＞0，判断f（x）在

  （

  0

  ，

  1

  a

  ）

  的单调性，并用定义法证明；
  （3）若a=1，g（x）=f（e^x）-18，判断函数g（x）的零点个数，并说明理由．
  组卷：110引用：3难度：0.5

  解析