当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省苏州市常熟中学高二（下）调研数学试卷（5月份）

发布：2024/7/9 8:0:8

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若随机变量X服从正态分布N（3，σ²），且P（X≤4）=0.64，则P（2≤X≤3）=（　　）
A．0.07 B．0.14 C．0.28 D．0.36
组卷：32引用：2难度：0.7
解析
2．已知集合
A
=
{
x
|
y
=
1
x
}
，
B
=
{
y
|
y
=
ln
1
-
x
}
，则A∩B=（　　）
A．∅ B．（0，+∞）
C．（0，1） D．（-∞，0）∪（0，+∞）
组卷：32引用：2难度：0.7
解析
3．已知a,b∈R，则使得“a＞b＞0”成立的一个充分不必要条件为（　　）
A．
1
a
＞
1
b
B．a³＞b³ C．
a
-
1
＞
b
-
1
D．lna＞lnb
组卷：48引用：2难度：0.7
解析
4．“学如逆水行舟，不进则退；心似平原跑马，易放难收”（明•《增广贤文》）是勉励人们专心学习的．如果每天的“进步”率都是1%，那么一年后是（1+1%）³⁶⁵=1.01³⁶⁵；如果每天的“退步”率都是1%，那么一年后是（1-1%）³⁶⁵=0.99³⁶⁵.一年后“进步”的是“退步”的
1
.
01
365
0
.
99
365
=
（
1
.
01
0
.
99
）
365
≈
1481
倍．如果每月的“进步”率和“退步”率都是20%，那么大约经过（　　）月后“进步”的是“退步”的一万倍．（lg2≈0.3010，lg3≈0.4771）
A．20 B．21 C．22 D．23
组卷：306引用：9难度：0.8
解析
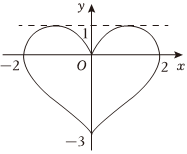5．如图所示的“心形”图形可看作由两个函数的图象构成，则“心形”图形在x轴上方的图象对应的函数解析式可能为（　　）
A．
y
=
-
x
2
+
2
|
x
|
B．
y
=
x
4
-
x
2
C．
y
=
|
x
|
4
-
x
2
D．
y
=
-
x
2
+
2
x
组卷：92引用：3难度：0.6
解析
6．已知函数f（x-1）为偶函数，且函数f（x）在[-1，+∞）上单调递增，则关于x的不等式f（1-2^x）＜f（-7）的解集为（　　）
A．（-∞，3） B．（3，+∞） C．（-∞，2） D．（2，+∞）
组卷：217引用：6难度：0.6
解析
7．若（mx-1）ⁿ（n∈N^*）的展开式中，所有项的系数和与二项式系数和相等，且第6项的二项式系数最大，则有序实数对（m,n）共有（　　）组不同的解．
A．1 B．2 C．3 D．4
组卷：229引用：7难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.

21．甲、乙，丙三位学徒跟师傅学习制作某种陶器，经过一段时间的学习后，他们各自能制作成功该陶器的概率分别为p₁，p₂，p₃，且0＜p₃＜p₂＜p₁＜1，现需要他们三人制作一件该陶器，每次只有一个人制作且每个人只制作一次，如果有一个人制作失败则换下一个人重新制作，若陶器制作成功则结束．
（1）按甲、乙、丙的顺序制作陶器，若
p
1
p
2
=
2
9
，
p
1
∈
[
2
3
，
1
）
，求制作陶器人数X的数学期望的最大值．
（2）若这种陶器制作成功后需要检测合格才能上市销售，如果这种陶器可以上市销售，则每件陶器可获利100元；如果这种陶器不能上市销售，则每件陶器亏损80元，已知甲已经制成了4件这种陶器，且甲制作的陶器检测合格的概率为
2
5
，求这4件陶器最终盈亏Y的概率分布和数学期望．
组卷：36引用：4难度：0.5
解析
22．已知函数f（x）=axe^x-ln（x+1）（a∈R）．
（1）讨论f（x）的极值点的个数；
（2）若f（x）≥2lna-3ln2-3恒成立，求实数a的最大值．
组卷：39引用：2难度：0.3
解析