2023-2024学年河南省焦作市博爱一中高三(上)期中数学试卷
发布:2024/9/28 3:0:4
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知函数f(x)=
,若f(x)在R上是增函数,则实数a的取值范围是( )-x2+4ax,x≤1(2a+3)x-4a+5,x>1组卷:581引用:10难度:0.8 -
2.已知a=log50.2,b=log0.50.2,c=0.50.2,则a,b,c的大小关系为( )
组卷:128引用:3难度:0.8 -
3.已知函数f(x)=sin(ωx+φ)在区间
单调递增,直线(π6,2π3)和x=π6为函数y=f(x)的图象的两条对称轴,则f(0)=( )x=2π3组卷:254引用:6难度:0.7 -
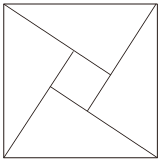 4.赵爽弦图是中国古代数学的重要发现,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).已知小正方形的面积为1,直角三角形中较小的锐角为θ,且,则大正方形的面积为( )tanθ2=13组卷:97引用:5难度:0.6
4.赵爽弦图是中国古代数学的重要发现,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).已知小正方形的面积为1,直角三角形中较小的锐角为θ,且,则大正方形的面积为( )tanθ2=13组卷:97引用:5难度:0.6 -
5.若直线l:(a-2)x+ay+2a-3=0经过第四象限,则a的取值范围为( )
组卷:370引用:2难度:0.5 -
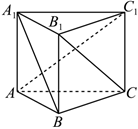 6.如图,在直三棱柱ABC-A1B1C1中,AB=BC=a,,直线AC1与平面A1B1C1所成角的正弦值为AA1=2a,则异面直线BA1与B1C所成角的余弦值为( )105组卷:116引用:5难度:0.5
6.如图,在直三棱柱ABC-A1B1C1中,AB=BC=a,,直线AC1与平面A1B1C1所成角的正弦值为AA1=2a,则异面直线BA1与B1C所成角的余弦值为( )105组卷:116引用:5难度:0.5 -
7.设数列{an}是以d为公差的等差数列,Sn是其前n项和,a1>0,且S5=S8,则下列结论正确的是( )
组卷:616引用:9难度:0.5
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.已知函数f(x)=-x2+ax-lnx
(1)判断f(x)的单调性;
(2)若函数f(x)存在极值,求这些极值的和的取值范围.组卷:180引用:5难度:0.5 -
22.已知a∈R,复数z1=a-1+i,z2=1-
=-1在复平面上对应的点分别为A、B、C,O为坐标原点.a+2ai,z3
(1)求|z1+z2|的取值范围;
(2)当A、B、C三点共线时,求三角形AOB的面积.组卷:246引用:7难度:0.7


