当前位置：试卷中心 > 试卷详情

2022-2023学年四川省攀枝花市西区八年级（上）期中数学试卷

发布：2024/8/27 1:0:9

一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．9的平方根是（　　）
A．3 B．-3 C．±3 D．
±
3
组卷：3696引用：41难度：0.8
解析
2．下列运算中，结果正确的是（　　）
A．a³•a⁴=a¹² B．（a²）³=a⁵ C．a⁶÷a²=a⁴ D．a³+a²=a⁵
组卷：197引用：11难度：0.7
解析
3．与数轴上的点一一对应的数是（　　）
A．正数 B．负数 C．有理数 D．实数
组卷：6引用：1难度：0.7
解析
4．在实数4，0，
12
7
，
3
0
.
125
，0.1010010001，
3
，
π
2
中无理数有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：340引用：6难度：0.9
解析
5．下列命题是真命题的是（　　）
A．直角都相等 B．若a²=b²，则a=b
C．相等的角是对顶角 D．同位角相等
组卷：37引用：3难度：0.6
解析
6．下列计算中，正确的是（　　）
A．2a²•3a³=6a⁶
B．（a+b）（a-b）=a²-b²
C．（a+b）²=a²+b²
D．（6a⁴-4a³+2a）÷2a=3a³-2a²
组卷：14引用：1难度：0.5
解析
7．若（x+2）（x-1）=x²+mx+n,则m+n=（　　）
A．1 B．-2 C．-1 D．2
组卷：238引用：7难度：0.7
解析
8．估计
7
+1的值（　　）
A．在1和2之间 B．在2和3之间 C．在3和4之间 D．在4和5之间
组卷：3026引用：60难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（解答应写出文字说明、证明过程或演算步骤．17题-22题每小题8分，23题每小题8分，24题12分，共70分）

23．阅读以下材料：
苏格兰数学家纳皮尔（J．Npler,1550-1617年）是对数的创始人．他发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evler,1707-1783年）才发现指数与对数之间的联系．
对数的定义：一般地，若a^x=N（a＞0且a≠1），那么x叫做以a为底N的对数，记作x=log_aN，比如指数式2⁴=16可以转化为对数式4=log₂16，对数式2=log₃9可以转化为指数式3²=9．
我们根据对数的定义可得到对数的一个性质：
log_a（M•N）=log_aM+log_aN（a＞0，a≠1，M＞0，N＞0），理由如下：
设log_aM=m,log_aN=n,则M=a^m，N=aⁿ，
∴M•N=a^m•aⁿ=a^m+n，由对数的定义得m+n=log_a（M•N）．
又∵m+n=log_aM+log_aN，
∴log_a（M•N）=log_aM+log_aN．
根据上述材料，结合你所学的知识，解答下列问题：
（1）填空：①log₂32=
，②log₃27=
，③log₇1=
；
（2）求证：log_a
M
N
=log_aM-log_aN（a＞0，a≠1，M＞0，N＞0）；
（3）拓展运用：计算log₅125+log₅6-log₅30．
组卷：1441引用：22难度：0.6
解析
24．在图1、图2、图3、图4中，点P在线段BC上移动（不与B、C重合），M在BC的延长线上．
（1）如图1，△ABC和△APE均为正三角形，连接CE．
①求证：△ABP≌△ACE．
②∠ECM的度数为
°．
（2）①如图2，若四边形ABCD和四边形APEF均为正方形，连接CE．则∠ECM的度数为
°．
②如图3，若五边形ABCDF和五边形APEGH均为正五边形，连接CE．则∠ECM的度数为
°．
（3）如图4，n边形ABC…和n边形APE…均为正n边形，连接CE，请你探索并猜想∠ECM的度数与正多边形边数n的数量关系（用含n的式子表示∠ECM的度数），并利用图4（放大后的局部图形）证明你的结论．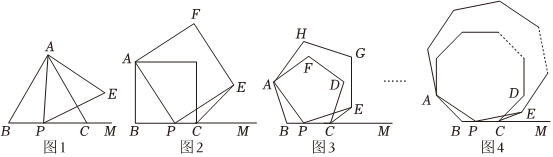
组卷：1536引用：9难度：0.1
解析