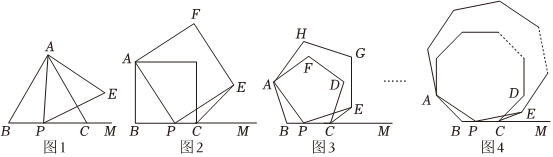
在图1、图2、图3、图4中，点P在线段BC上移动（不与B、C重合），M在BC的延长线上．
（1）如图1，△ABC和△APE均为正三角形，连接CE．
①求证：△ABP≌△ACE．
②∠ECM的度数为 6060°．
（2）①如图2，若四边形ABCD和四边形APEF均为正方形，连接CE．则∠ECM的度数为 4545°．
②如图3，若五边形ABCDF和五边形APEGH均为正五边形，连接CE．则∠ECM的度数为 3636°．
（3）如图4，n边形ABC…和n边形APE…均为正n边形，连接CE，请你探索并猜想∠ECM的度数与正多边形边数n的数量关系（用含n的式子表示∠ECM的度数），并利用图4（放大后的局部图形）证明你的结论．
【考点】四边形综合题．
【答案】60；45；36
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/27 1:0:9组卷：1536引用：9难度：0.1
相似题
-
1．天府新区某校数学活动小组在一次活动中，对一个数学问题作如下探究：
（1）问题发现：如图1，在等边△ABC中，点P是边BC上任意一点，连接AP，以AP为边作等边△APQ，连接CQ．求证：BP=CQ；
（2）变式探究：如图2，在等腰△ABC中，AB=BC，点P是边BC上任意一点，以AP为腰作等腰△APQ，使AP=PQ，∠APQ=∠ABC，连接CQ．判断∠ABC和∠ACQ的数量关系，并说明理由；
（3）解决问题：如图3，在正方形ADBC中，点P是边BC上一点，以AP为边作正方形APEF，Q是正方形APEF的中心，连接CQ．若正方形APEF的边长为6，CQ=2，求正方形ADBC的边长．2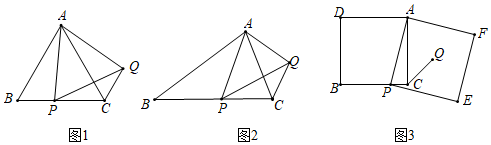
发布：2025/6/13 22:0:1组卷：2504引用：13难度：0.2 -
2．已知，如图：在直角坐标系中，正方形AOBC的边长为4，点D，E分别是线段AO，BO上的动点，D点由A点向O点运动，速度为每秒1个单位，E点由B点向O点运动，速度为每秒2个单位，当一个点停止运动时，另一个点也随之停止，设运动时间为t（秒）
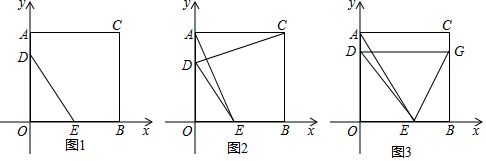
（1）如图1，当t为何值时，△DOE的面积为6；
（2）如图2，连接CD，与AE交于一点，当t为何值时，CD⊥AE；
（3）如图3，过点D作DG∥OB，交BC于点G，连接EG，当D，E在运动过程中，能否使得点D，E，G三点构成等腰三角形，如果能，请直接写出t的值．发布：2025/6/13 20:30:1组卷：97引用：8难度：0.3 -
3．在矩形ABCD中，E是直线BC上一动点．
（1）如图1，当BE=AB时，过点A作AP⊥DE于点P，连接BP，求∠BPE的度数；
（2）如图2，若F、G分别为AE、BC的中点，FG与ED相交于点H，求证：HE=HG；
（3）如图3，若AB=BC，过点C作CH⊥AE，垂足为H，连接DH，若∠CDH=22.5°．则的值为 （直接写出结果）．CHAH
发布：2025/6/13 21:0:2组卷：158引用：1难度：0.1
