2023-2024学年北京市大兴一中高二（上）月考数学试卷（10月份）
发布：2024/9/12 5:0:8
一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.
-
1．已知点M在平面ABC内，并且对空间任一点O，
则x的值为（ ）OM=xOA+12OB+13OC组卷：288引用：26难度：0.9 -
2．给出下列命题，其中说法正确的是（ ）
组卷：145引用：3难度：0.8 -
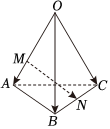3．如图，在四面体OABC中，，OA=a，OB=b．点M在OA上，且OM=2MA，N为BC中点，则OC=c等于（ ）MN组卷：431引用：74难度：0.7 -
4．一袋中装有大小相同，编号分别为1，2，3，4，5，6，7，8的八个球，从中有放回地每次取一个球，共取2次，则取得两个球的编号和不小于15的概率为（ ）
组卷：640引用：15难度：0.7 -
5．先后两次掷一枚质地均匀的骰子，事件A=“两次掷出的点数之和是6”，事件B=“第一次掷出的点数是奇数”，事件C=“两次掷出的点数相同”，则（ ）
组卷：461引用：8难度：0.7 -
6．在正四面体P-ABC中，棱长为1，且D为棱AB的中点，则
的值为（ ）PC•PD组卷：1097引用：8难度：0.8 -
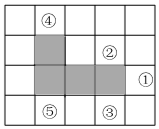7．如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是（ ）组卷：48引用：2难度：0.7
三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.
-
20．如图1，在四边形ABCD中，AD∥BC，BC=2AD．E，F分别为AD，BC的中点，AE=EF=1，AF=
AE．将四边形ABFE沿EF折起，使平面ABFE⊥平面EFCD（如图2）G是BF的中点．2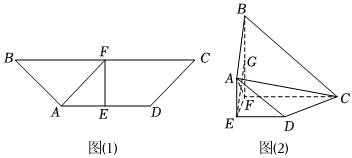
（1）证明：AC⊥EG；
（2）在线段BC上是否存在一点H，使得DH∥平面ABFE？若存在，求的值；若不存在，说明理由；BHBC
（3）证明：平面DAC⊥平面ACF．组卷：76引用：1难度：0.4 -
21．设全体空间向量组成的集合为V，
为V中的一个单位向量，建立一个“自变量”为向量，“应变量”也是向量的“向量函数”a=（a1，a2，a3）．f（x）：f（x）=-x+2（x•a）a（x∈V）
（1）设，u=（1，0，0），若v=（0，0，1），求向量f（u）=v；a
（2）对于V中的任意两个向量，x，证明：y；f（x）•f（y）=x•y
（3）对于V中的任意单位向量，求x的最大值．|f（x）-x|组卷：92引用：4难度：0.5
