2022-2023学年陕西省榆林市横山中学高二（下）期中数学试卷（文科）

一、选择题：本大题共12小题．每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合要求的.

• 1．命题：∀x∈R，x+lnx＞0的否定是（　　）

  A．∀x∉R，x+lnx＞0	B．∀x∉R，x+lnx≤0
  C．∃x∈R，x+lnx＞0	D．∃x∈R，x+lnx≤0
  组卷：151引用：5难度：0.8

  解析

• 2．已知集合A={x|x²＜8}，B={x|1-x≤0}，则A∩B=（　　）

  A．[-1，2）

  B． [ 1 ， 2 2 ）

  C．[1，2）

  D．[0，3）
  组卷：171引用：6难度：0.8

  解析

• 3．已知复数z满足i（z+1）=-1+2i（其中i为虚数单位），则

  z

  =（　　）

  A．1-i

  B．1+i

  C．-3-i

  D．-3+i
  组卷：64引用：3难度：0.8

  解析

• 4．点P的直角坐标为

  （

  -

  2

  ，

  2

  ）

  ，那么它的极坐标可表示为（　　）

  A． （ 2 ， 3 π 4 ）

  B． （ 2 ， 5 π 4 ）

  C． （ 1 ， 5 π 4 ）

  D． （ 1 ， 3 π 4 ）
  组卷：24引用：1难度：0.9

  解析

• 5．已知均为实数a,b,c,d,且a＞b＞0＞c＞d,则下列不等式成立的是（　　）

  A．a2＞c2	B．ln（ab）＞ln（cd）
  C． c a ＞ d b	D．2-c＞2-d
  组卷：39引用：1难度：0.7

  解析

• 6．已知复数z满足

  2

  （

  z

  -

  z

  ）

  +

  z

  •

  z

  =

  2

  +

  4

  i

  ，z在复平面内对应的点在第二象限，则z=（　　）

  A．-1-i

  B．1+i

  C．-1+i

  D．-2+i
  组卷：116引用：5难度：0.8

  解析

• 7．已知直线的参数方程为

  x = 3 - tsin 20 °

  y = 2 + tcos 70 °

  ，则该直线的倾斜角为（　　）

  A．20°

  B．45°

  C．110°

  D．135°
  组卷：78引用：3难度：0.7

  解析

三、解答题（本大题共6小题，共70分解答应写出文字说明、证明过程或演算步骤）

• 21．在平面直角坐标系xOy中，直线l₁的参数方程为

  x = t

  y = kt

  （t为参数），直线l₂的参数方程为

  x = - km + 2

  y = m

  （m为参数），设直线l₁与l₂的交点为P，当k变化时点P的轨迹为曲线C₁．
  （Ⅰ）求曲线C₁的轨迹方程；
  （Ⅱ）以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线C₂的极坐标方程为ρsin（θ+

  π

  4

  ）=3

  2

  ，点Q为曲线C₁上的动点，求点Q到直线C₂距离的最大值．
  组卷：16引用：1难度：0.4

  解析

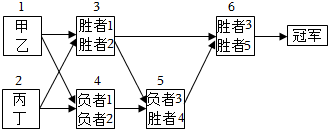• 22．甲、乙、丙、丁4名棋手进行象棋比赛，赛程如下面的框图所示，其中编号为i的方框表示第i场比赛，方框中是进行该场比赛的两名棋手，第i场比赛的胜者称为“胜者i”，负者称为“负者i”，第6场为决赛，获胜的人是冠军．已知甲每场比赛获胜的概率均为

  3

  4

  ，而乙、丙、丁相互之间胜负的可能性相同．
  （1）求乙获连负两场的概率；
  （2）求甲获得冠军的概率；
  （3）求乙进入决赛，且乙与其决赛对手是第二次相遇的概率．
  组卷：381引用：3难度：0.4

  解析