2022-2023学年湖南省益阳市桃江县高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．已知集合A={x|-5＜x＜5}，B={-1，3，4，5}，则A∩B的子集的个数为（　　）

  A．2

  B．3

  C．8

  D．16
  组卷：189引用：3难度：0.9

  解析

• 2．设复数

  z

  =

  i

  2

  -

  i

  ，则其共轭复数z在复平面上对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：8引用：1难度：0.8

  解析

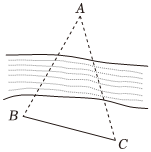• 3．如图，A，B两点在河流的两岸，在B同侧的河岸边选取点C，测得B，C两点间的距离为10米，∠ABC=75°，∠ACB=60°，则|AB|=（　　）

  A． 5 2 米

  B． 5 3 米

  C． 5 5 米

  D． 5 6 米
  组卷：37引用：1难度：0.9

  解析

• 4．若向量

  a

  =（m,1），

  b

  =（-1，3），则“m=1”是“

  a

  ⊥（

  a

  -

  b

  ）”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：99引用：2难度：0.7

  解析

• 5．已知α∈（0，π），且

  tanα

  =

  2

  2

  ，则

  tan

  α

  2

  =（　　）

  A． 2 4

  B． 2

  C． 2 2

  D． 2 2 3
  组卷：93引用：1难度：0.7

  解析

• 6．分别抛掷两枚质地均匀的硬币，设事件A表示“第一枚正面朝上”，事件B表示“两枚硬币朝上的面相同”，则A与B（　　）

  A．是互斥事件也是相互独立事件

  B．不互斥但相互独立

  C．是对立事件

  D．既不互斥也不相互独立
  组卷：49引用：2难度：0.8

  解析

• 7．已知球与圆台的上下底面和侧面都相切．若圆台的侧面积为16π，上、下底面的面积之比为1：9，则球的表面积为（　　）

  A．12π

  B．14π

  C．16π

  D．18π
  组卷：389引用：7难度：0.5

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

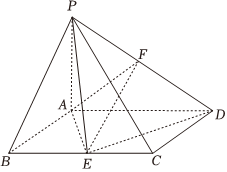• 21．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是矩形，AB=2，BC=4，E，F分别为BC，PD的中点．
  （1）证明：EF∥平面PAB；
  （2）证明：平面PAE⊥平面PDE；
  （3）若PA与平面PED所成角的正切值为

  2

  ，求点C到平面PDE的距离．
  组卷：84引用：1难度：0.5

  解析

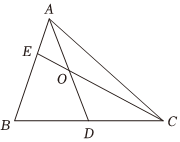• 22．如图，在△ABC中，AB=2，

  AC

  =

  11

  ，

  cos

  ∠

  BAC

  =

  5

  11

  22

  ，D为BC的中点，E为AB边上的动点（不含端点），AD与CE交于点O，

  AE

  =

  x

  AB

  ．
  （1）若

  x

  =

  1

  4

  ，求

  CO

  CE

  的值；
  （2）求

  AO

  •

  CE

  的最小值，并指出取到最小值时x的值．
  组卷：22引用：2难度：0.5

  解析