2023-2024学年贵州省遵义市八年级（上）月考数学试卷（10月份）
发布：2024/9/7 1:0:8
一、选择题。（本大题共12小题，每小题3分，共36分）
-
1．已知△ABC≌△DEF，∠A=40°，∠B=50°，则∠D的度数为（ ）
组卷：204引用：4难度：0.8 -
2．用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（ ）
组卷：7277引用：101难度：0.9 -
3．如图是某校门口的电动伸缩门，电动伸缩门利用了（ ）性质组卷：264引用：6难度：0.7 -
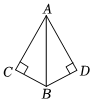4．如图，已知∠BCA=∠BDA=90°，BC=BD．则证明△BAC≌△BAD的理由是（ ）
组卷：322引用：5难度：0.7 -
5．一个多边形的每个外角都是72°，则这个多边形的边数为（ ）
组卷：572引用：8难度：0.8 -
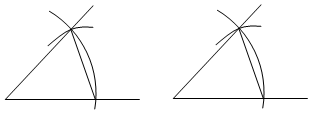6．如图，是尺规作图中“画一个角等于已知角”的示意图，该作法运用了“全等三角形的对应角相等”这一性质，则判定图中两三角形全等的条件是（ ）组卷：4633引用：55难度：0.5 -
7．四根木棒的长度分别为5cm,6cm,9cm,13cm,现从中取三根，使它们首尾顺次相接组成一个三角形，则这样的取法共有（ ）
组卷：213引用：4难度：0.7 -
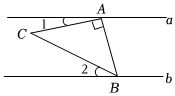8．如图，直线a∥b,Rt△ABC的直角顶点A落在直线a上，点B落在直线b上，若∠1=15°，∠2=25°，则∠ABC的大小为（ ）组卷：3125引用：23难度：0.6
三、解答题。（本大题共9小题，共98分，解答要写出必要的文字说明、证明过程或演算步骤）
-
24．在△ABC中，D是BC边上的点（不与点B、C重合），连接AD．
（1）如图①，当点D是BC边上的中点时，S△ABD：S△ACD=；
（2）如图②，当AD是∠BAC的平分线时，若AB=m,AC=n,求S△ABD：S△ACD的值（用含m,n的代数式表示）；
（3）如图③，AD平分∠BAC，延长AD到E，使得AD=DE，连接BE，如果AC=2，AB=4，S△BDE=6，求S△ABC的值．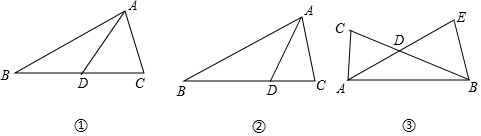
组卷：778引用：7难度：0.4 -
25．如图（1）．AE与BD相交于点C．AC=EC，BC=DC，AB=4cm,点P从点A出发，沿A——B——A的路径以3cm/s的速度运动；方向以tcm/s的速度运动；点Q从点D出发，沿D——E的方向以1cm/s的速度运动，P、Q两点同时出发，当点P到达点A时，P、Q两点同时停止运动，设运动时间为t（s）．
（1）求证：AB∥DE；
（2）用含t的式子表示线段AP的长；
（3）连接PQ，当线段PQ经过点C时（如图2）．求t的值．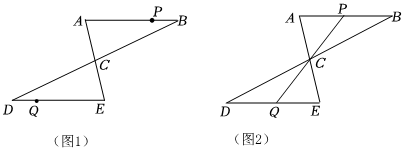
组卷：181引用：2难度：0.5
