2022-2023学年云南省昆明市五华区七年级（下）期末数学试卷

一、选择题（本大题共12小题，每小题只有一个正确选项，每小题3分，共36分）

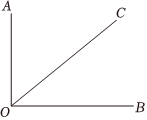• 1．如图，AO⊥OB于点O，若∠BOC=40°，则∠AOC的度数是（　　）

  A．40°A

  B．40°

  C．50°

  D．60°
  组卷：94引用：1难度：0.7

  解析

• 2．下列实数中，是无理数的是（　　）

  A． - 1 16

  B．3.14159

  C． 22 7

  D． 3 9
  组卷：89引用：1难度：0.8

  解析

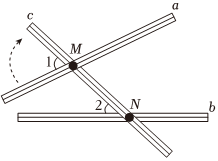• 3．如图，用大头针把3根平放在桌面上的细直木条分别固定在M，N处，并使木条可以绕点M，N转动，若∠1=70°，∠2=50°，只转动木条a使其与b平行，则木条a旋转的度数至少是（　　）

  A．10°

  B．20°

  C．50°

  D．70°
  组卷：107引用：2难度：0.7

  解析

• 4．下列计算正确的是（　　）

  A． 3 - 8 = - 2

  B． 9 =± 3

  C． （ - 3 ） 2 = - 3

  D． （ - 5 ） 2 = - 5
  组卷：136引用：1难度：0.8

  解析

• 5．如果x,y满足方程组

  x + y = - 1

  2 x - y = 7

  ，那么x-2y的值是（　　）

  A．-2

  B．2

  C．-8

  D．8
  组卷：212引用：3难度：0.8

  解析

• 6．若3x＞-3y,则下列不等式中一定成立的是（　　）

  A．x+y＞0

  B．x-y＞0

  C．x+y＜0

  D．x-y＜0
  组卷：500引用：9难度：0.8

  解析

• 7．为了解2023年昆明市九年级学生学业水平考试的数学成绩，从中随机抽取了1000名学生的数学成绩，下列说法正确的是（　　）

  A．2023年昆明市九年级学生是总体

  B．每一名九年级学生是个体

  C．1000名九年级学生是总体的一个样本

  D．样本容量是1000
  组卷：489引用：9难度：0.9

  解析

• 8．一个不等式组中的两个不等式的解集如图所示，则这个不等式组的解集是（　　）

  A．-2＜x＜1

  B．-2＜x≤1

  C．-2≤x＜1

  D．-2≤x≤1
  组卷：160引用：3难度：0.8

  解析

三、解答题（本大题共8小题，共56分）

• 23．小明在一组平行线中作角，探究角的两边与平行线形成的锐角的数量关系．
  （1）如图1，他先作出∠AOB=60°．且点O在一条直线上，当∠1=19°时，∠2=41°．若点O在两条平行线之间，如图2．请你用等式表示∠1与∠2的数量关系并证明；
  （2）在图3中．∠AOB=60°，点O在两条平行线之间．记OA与图中一条直线形成的锐角为α，若小明作射线OC，使得∠COB=45°，记OC与图中另一条直线形成的锐角为β．请用等式表示α与β之间的数量关系．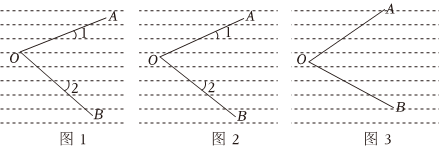
  组卷：117引用：1难度：0.5

  解析

• 24．阅读材料：
  我们知道|x|是数轴上表示数x的点到原点的距离，即|x|=|x-0|，这个结论可推广为|x₁-x₂|是数轴上表示数x₁，x₂的两点之间的距离．
  例1：解方程|x|=6．
  解：∵|x|=|x-0|=6，
  又∵在数轴上与原点距离为6的点对应的数为±6，
  ∴方程的解为x=±6．
  例2：解不等式|x-1|＞2．
  解：先求方程|x-1|=2的解，如图，在数轴上找出到表示1的点的距离为2的点，它们对应的数分别为-1，3，所以|x-1|＞2的解集是到表示数1的点的距离大于2的所有点对应的数，则原不等式的解集为x＜-1或x＞3．
  
  参考阅读材料，解答下列问题：
  （1）方程|x-5|=3的解为

  ；
  （2）解不等式2|x+2|+1＜9；
  （3）若|x-1|+|x+2|=3，求x的取值范围；
  （4）若y=|x-1|-|x+2|，求y的取值范围．
  组卷：219引用：1难度：0.6

  解析