2022-2023学年山东省德州市宁津县八年级(下)期末数学试卷
发布:2024/6/30 8:0:9
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,
-
1.若二次根式
有意义,则x的取值范围是( )x-6组卷:286引用:9难度:0.8 -
2.为了解美食节同学们最喜爱的菜肴,需要获取的统计量是( )
组卷:247引用:6难度:0.7 -
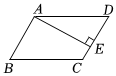 3.如图,在平行四边形ABCD中,AE⊥CD于点E,∠B=65°,则∠DAE等于( )组卷:294引用:7难度:0.7
3.如图,在平行四边形ABCD中,AE⊥CD于点E,∠B=65°,则∠DAE等于( )组卷:294引用:7难度:0.7 -
4.如图,小红家的木门左下角有一点受潮,她想检测门是否变形,准备采用如下方法:先测量门的边AB和BC的长,再测量点A和点C间的距离,由此可推断∠B是否为直角,这样做的依据是( )
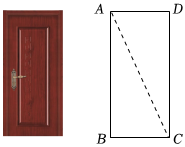 组卷:1100引用:13难度:0.5
组卷:1100引用:13难度:0.5 -
5.在同一坐标系中,函数y=kx与y=x-k的图象大致是( )
组卷:3693引用:20难度:0.6 -
6.下列运算正确的是( )
组卷:68引用:3难度:0.8 -
7.下列性质中,菱形具有而矩形不一定具有的是( )
组卷:23引用:1难度:0.5 -
 8.图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC=2,且∠AOB=30°,则OC的长度为( )组卷:563引用:16难度:0.7
8.图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC.若AB=BC=2,且∠AOB=30°,则OC的长度为( )组卷:563引用:16难度:0.7
三、解答题:本大题共7小题,共78分.
-
24.勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)证明勾股定理
据传当年毕达哥拉斯借助如图3所示的两个图验证了勾股定理,请你说说其中的道理.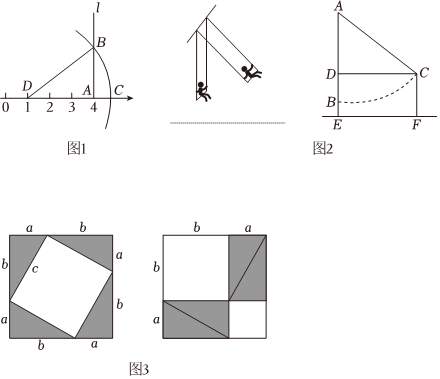
(2)应用勾股定理
①应用场景1——在数轴上画出表示无理数的点.
如图1,在数轴上找出表示4的点A,过点A作直线l垂直于DA,在l上取点B,使AB=2,以点D为圆心,DB为半径作弧,则弧与数轴的交点C表示的数是 .
②应用场景2——解决实际问题.
如图2,郑州某公园有一秋千,秋千静止时,踏板离地的垂直高度BE=0.5m,将它往前推2m至C处时,水平距离CD=2m,踏板离地的垂直高度CF=1.5m,它的绳索始终拉直,求绳索AC的长.组卷:353引用:5难度:0.5 -
25.(1)对于试题“如图①,在正方形ABCD中,E、F分别是BC、DC上的点,且∠EAF=45°,连接EF,探究BE、DF、EF之间的数量关系”,数学王老师给出了如下的思路:
请根据数学王老师的思路探究BE、DF、EF之间的数量关系,并说明理由;延长CB到M,使得BM=DF,连接AM,……,利用三角形全等的判定及性质解答,……
(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、DC上的点,且∠EAF=∠BAD,此时(1)中的结论是否仍然成立?请说明理由.12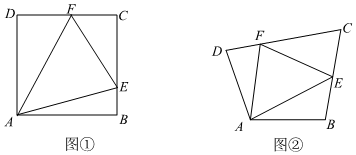 组卷:480引用:4难度:0.5
组卷:480引用:4难度:0.5


