勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一,它不但因证明方法层出不穷吸引着人们,更因为应用广泛而使人入迷.
(1)证明勾股定理
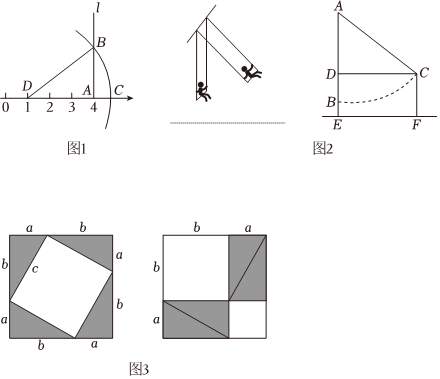
据传当年毕达哥拉斯借助如图3所示的两个图验证了勾股定理,请你说说其中的道理.
(2)应用勾股定理
①应用场景1——在数轴上画出表示无理数的点.
如图1,在数轴上找出表示4的点A,过点A作直线l垂直于DA,在l上取点B,使AB=2,以点D为圆心,DB为半径作弧,则弧与数轴的交点C表示的数是 13+113+1.
②应用场景2——解决实际问题.
如图2,郑州某公园有一秋千,秋千静止时,踏板离地的垂直高度BE=0.5m,将它往前推2m至C处时,水平距离CD=2m,踏板离地的垂直高度CF=1.5m,它的绳索始终拉直,求绳索AC的长.
13
13
【答案】+1
13
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/3 8:0:9组卷:353引用:5难度:0.5
相似题
-
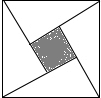 1.由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )发布:2025/6/15 7:30:2组卷:2199引用:8难度:0.9
1.由四个全等的直角三角形如图所示的“赵爽弦图”,若直角三角形斜边长为2,一个锐角为30°,则图中阴影部分的面积为( )发布:2025/6/15 7:30:2组卷:2199引用:8难度:0.9 -
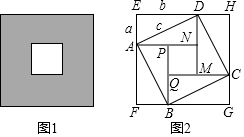 2.小颖用四块完全一样的长方形方砖,恰好拼成如图1所示图案,如图2,连接对角线后,她发现该图案中可以用“面积法”采用不同方案去证明勾股定理.设AE=a,DE=b,AD=c,请你找到其中一种方案证明:a2+b2=c2.发布:2025/6/15 2:30:1组卷:617引用:2难度:0.5
2.小颖用四块完全一样的长方形方砖,恰好拼成如图1所示图案,如图2,连接对角线后,她发现该图案中可以用“面积法”采用不同方案去证明勾股定理.设AE=a,DE=b,AD=c,请你找到其中一种方案证明:a2+b2=c2.发布:2025/6/15 2:30:1组卷:617引用:2难度:0.5 -
3.利用下面的图形分别给出勾股定理的两种证明.
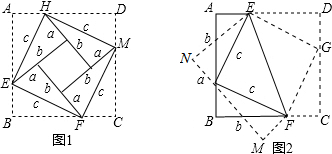 发布:2025/6/15 6:0:1组卷:233引用:2难度:0.5
发布:2025/6/15 6:0:1组卷:233引用:2难度:0.5


