当前位置：试卷中心 > 试卷详情

2023-2024学年湖南省长沙市长郡中学高二（上）期中数学试卷

发布：2024/10/3 15:0:2

一、选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1．若两个不同平面α，β的法向量分别为
u
=（1，2，-1），
v
=（-3，-6，3），则（　　）
A．α∥β B．α⊥β
C．α，β相交但不垂直 D．以上均不正确
组卷：302引用：9难度：0.9
解析
2．《莱因德纸草书》（RhindPapyrus）是世界上最古老的数学著作之一，书中有一道这样的题目，请给出答案：把100个面包分给5个人，使每人所得面包个数成等差数列，且使较大的三份之和的
1
7
是较小的两份之和，则最小的一份为（　　）
A．
5
3
B．
10
3
C．
5
6
D．
11
6
组卷：151引用：2难度：0.7
解析
3．若直线y=kx-2与直线y=3x垂直，则k=（　　）
A．3 B．
1
3
C．-3 D．
-
1
3
组卷：114引用：2难度：0.8
解析
4．直三棱柱ABC-A₁B₁C₁中，∠BCA=90°，M，N分别是A₁B₁，A₁C₁的中点，BC=CA=CC₁，则BM与NA所成的角的余弦值为（　　）
A．
-
30
10
B．
30
6
C．
30
10
D．
2
2
组卷：101引用：3难度：0.5
解析
5．双曲线C与椭圆
x
2
9
+
y
2
4
=
1
有相同的焦点，一条渐近线的方程为x-2y=0，则双曲线C的标准方程为（　　）
A．
x
2
4
-
y
2
=
1
B．
y
2
9
-
x
2
36
=
1
C．
x
2
9
-
y
2
36
=
1
D．
y
2
4
-
x
2
=
1
组卷：375引用：10难度：0.7
解析
6．已知抛物线E：x²=4y和圆F：x²+（y-1）²=1，过点F作直线l与上述两曲线自左而右依次交于点A，C，D，B，则|AC|与|BD|的乘积为（　　）
A．1 B．2 C．3 D．
2
组卷：95引用：1难度：0.6
解析
7．已知数列{a_n}满足
2
a
n
+
1
a
n
+
a
n
+
1
-
3
a
n
=
0
（
n
∈
N
*
）
且a₁＞0．若{a_n}是递增数列，则a₁的取值范围是（　　）
A．
（
0
，
1
2
）
B．
（
1
2
，
1
）
C．（0，1） D．
（
0
，
2
-
1
）
组卷：127引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70分.解答时应写出必要的文字说明、证明过程或演算步骤）

21．已知数列{a_n}，a₁=2，
a
n
+
1
=
2
-
1
a
n
，数列{b_n}满足b₁=1，
b
2
n
b
2
n
-
1
=
b
2
n
+
1
b
2
n
=
a
n
．
（1）求证：数列
{
1
a
n
-
1
}
为等差数列，并求出数列{a_n}的通项公式；
（2）求b_2n+1的表达式；
（3）求证：
1
b
2
+
1
b
4
+
…
+
1
b
2
n
＜
1
．
组卷：141引用：2难度：0.5
解析
22．已知椭圆C：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
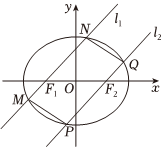的左、右焦点分别为F₁、F₂，焦距为2，上、下顶点分别为B₁、B₂，A为椭圆上的点，且满足
k
A
B
1
•
k
A
B
2
=
-
3
4
．
（1）求椭圆C的标准方程；
（2）过F₁、F₂作两条相互平行的直线l₁，l₂交C于M，N和P，Q，顺次连接构成四边形PQNM，求四边形PQNM面积的取值范围．
组卷：163引用：2难度：0.5
解析