2022-2023学年江西省宜春市樟树市清江中学高一(下)期中数学试卷
发布:2024/7/4 8:0:9
一、单选题(每题5分,共40分)
-
1.已知点(1,2)在α的终边上,则cosα=( )
组卷:228引用:4难度:0.8 -
2.已知向量
,a=(-1,2),若b=(3,λ)与a+2b平行,则实数λ的值为( )2a-b组卷:325引用:7难度:0.7 -
3.cos78°cos18°+sin78°sin18°的值为( )
组卷:94引用:2难度:0.9 -
4.函数
的最小值和最小正周期分别是( )f(x)=cos(2x+π6)组卷:213引用:3难度:0.9 -
5.将函数
的图象上各点向右平移f(x)=3sin(13x+π12)个单位长度得函数g(x)的图象,则g(x)的单调递增区间为( )π12组卷:77引用:2难度:0.7 -
6.已知函数
在[0,π]上恰有3个零点,则ω的取值范围是( )f(x)=2cos2ωx+3sin2ωx-1(ω>0)组卷:319引用:11难度:0.7 -
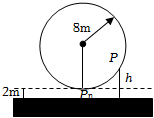 7.一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )组卷:63引用:3难度:0.7
7.一个大风车的半径为8m,12min旋转一周,它的最低点P0离地面2m,风车翼片的一个端点P从P0开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )组卷:63引用:3难度:0.7
四、解答题(共70分)
-
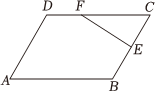 21.如图,在平行四边形ABCD中,∠BAD=60°,,BE=12BC.CF=2FD
21.如图,在平行四边形ABCD中,∠BAD=60°,,BE=12BC.CF=2FD
(1)若,求3x+2y的值;EF=xAB+yAD
(2)若,|AB|=6,求边AD的长.AC•EF=-18组卷:59引用:5难度:0.5 -
22.已知O为坐标原点,对于函数f(x)=asinx+bcosx,称向量
为函数f(x)的伴随向量,同时称函数f(x)为向量OM=(a,b)的伴随函数.OM
(1)设函数,试求g(x)的伴随向量的坐标;g(x)=sin(x+5π6)+cos(3π2+x)
(2)记向量的伴随函数为f(x),当ON=(1,3)且f(x)=85时,求sinx的值;x∈(-π3,π6)
(3)设向量,λ∈R的伴随函数为u(x),OP=(2λ,-2λ)的伴随函数为v(x),记函数h(x)=u(x)+v2(x),求h(x)在[0,π]上的最大值.OQ=(1,1)组卷:67引用:6难度:0.5


