2023-2024学年黑龙江省大庆市实验中学实验二部高二（上）段考数学试卷（10月份）

一、单选题（共8小题，每小题5分.每小题只有一项是符合题目要求的）

• 1．已知

  z

  =

  1

  +

  2

  i

  1

  -

  i

  （i为虚数单位），则

  z

  的虚部为（　　）

  A． - 3 2 i

  B． - 3 2

  C． - 1 2

  D． 3 2
  组卷：21引用：3难度：0.8

  解析

• 2．方程x²+y²+Dx+Ey+F=0表示以（-2，3）为圆心，4为半径的圆，则D，E，F的值分别为（　　）

  A．4，-6，3

  B．-4，6，3

  C．-4，-6，3

  D．4，-6，-3
  组卷：336引用：7难度：0.9

  解析

• 3．点D（-2，-2）到直线l：2x-y+mx-m=0（m∈R）距离的最大值为（　　）

  A．5

  B． 5

  C． 2 2

  D．3
  组卷：363引用：5难度：0.5

  解析

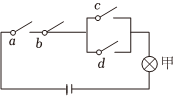• 4．如图所示的电路有a,b,c,d四个开关，每个开关断开与闭合的概率均为

  1

  2

  且是相互独立的，则灯泡甲亮的概率为（　　）

  A． 1 16

  B． 1 8

  C． 3 16

  D． 1 4
  组卷：48引用：2难度：0.8

  解析

• 5．坐标平面内有相异两点A（cosθ，sin²θ），B（0，1），经过两点的直线的倾斜角的取值范围是（　　）

  A． [ - π 4 ， π 4 ]	B． （ 0 ， π 4 ] ∪ [ 3 π 4 ， π ）
  C． [ 0 ， π 4 ] ∪ [ 3 π 4 ， π ）	D． [ π 4 ， 3 π 4 ]
  组卷：141引用：3难度：0.7

  解析

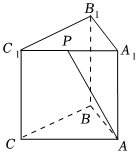• 6．如图，在直三棱柱ABC-A₁B₁C₁中，底面ABC是等腰直角三角形，AB⊥BC，AB=CC₁，P是A₁C₁的中点，则异面直线BC与AP所成角的余弦值为（　　）

  A．0

  B． 1 6

  C． 6 6

  D． 30 6
  组卷：533引用：5难度：0.7

  解析

• 7．△ABC中，a,b,c是角A，B，C的对边，

  S

  △

  ABC

  =

  1

  2

  c

  （

  a

  -

  b

  ）

  ，其外接圆半径R=2，且

  4

  （

  si

  n

  2

  A

  -

  si

  n

  2

  B

  ）

  =

  （

  3

  a

  -

  b

  ）

  sin

  B

  ，则（1+sinA）（1-sinB）=（　　）

  A．1

  B． 5 6

  C． 3 4

  D． 2 3
  组卷：198引用：2难度：0.5

  解析

四、解答题（共70分.解答应写出文字说明、证明过程或演算步骤）

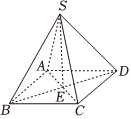• 21．在四棱锥S-ABCD中，已知底面ABCD为菱形，若BD⊥SC，AC⊥SD，BD∩AC=E．
  （1）求证：SE⊥平面ABCD；
  （2）若BD=

  3

  AC=2SE，设点H满足

  DH

  =μ

  DC

  （0＜μ＜1），当直线SC与平面SHE所成角的正弦值为

  7

  7

  时，求μ的值．
  组卷：146引用：3难度：0.6

  解析

• 22．某学校组织校园安全知识竞赛．在初赛中有两轮答题，第一轮从A类的5个问题中任选两题作答，若两题都答对，则得40分，否则得0分；第二轮从B类的5个问题中选两题作答，每答对1题得30分，答错得0分．如果两轮总积分不低于60分则晋级复赛．小芳和小明同时参赛，已知小芳每个问题答对的概率都为0.5．在A类的5个问题中，小明只能答对4个问题；在B类的5个问题中，小明每个问题答对的概率都为0.4．他们回答任一问题正确与否互不影响．
  （1）求小明在第一轮得40分的概率；
  （2）以晋级复赛的概率大小为依据，小芳和小明谁更容易晋级复赛？
  组卷：221引用：8难度：0.7

  解析