2022-2023学年江苏省徐州七中高二（上）学情调研数学试卷（9月份）

一、单项选择题（每题5分，共40分）

• 1．经过两点A（-3，2），B（0，-3）的直线的方程为（　　）

  A． y = 1 3 x - 3

  B． y = - 1 3 x - 3

  C． y = 5 3 x - 3

  D． y = - 5 3 x - 3
  组卷：783引用：5难度：0.8

  解析

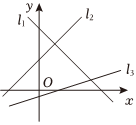• 2．若图中的直线l₁，l₂，l₃的斜率分别为k₁，k₂，k₃，则有（　　）

  A．k1＜k2＜k3

  B．k2＜k3＜k1

  C．k1＜k3＜k2

  D．k2＜k1＜k3
  组卷：482引用：8难度：0.7

  解析

• 3．椭圆

  x

  2

  m

  +

  y

  2

  4

  =1的焦距为2，则m的值等于（　　）

  A．3

  B．5

  C．8

  D．5或3
  组卷：1371引用：54难度：0.9

  解析

• 4．经过点P（2，-3）作圆C：x²+y²+2x=24的弦AB，使得点P平分弦AB，则弦AB所在直线的方程为（　　）

  A．x-y-5=0

  B．x+y-5=0

  C．x-y+5=0

  D．x+y+5=0
  组卷：380引用：5难度：0.7

  解析

• 5．直线y=x+b与曲线x=

  1

  -

  y

  2

  有且仅有一个公共点，则b的取值范围是（　　）

  A．b=±2	B．b=- 2 或-1＜b≤1
  C．-1≤b≤1	D．以上都不对
  组卷：179引用：5难度：0.6

  解析

• 6．若两条直线l₁：2x+ay-1=0与l₂：ax+（2a-1）y+3=0相互垂直，则a=（　　）

  A． - 1 2

  B．0

  C． - 1 2 或0

  D．-2或0
  组卷：213引用：5难度：0.8

  解析

• 7．数学家欧拉在1765年发现，任意三角形的外心、重心、垂心位于同一条直线上，这条直线称为欧拉线．已知△ABC的顶点A（2，0），B（0，4），若其欧拉线的方程为x-y+2=0，则顶点C的坐标为（　　）

  A．（-4，0）

  B．（-3，-1）

  C．（-5，0）

  D．（-4，-2）
  组卷：1064引用：17难度：0.6

  解析

四、解答题（共70分）

• 21．已知直线l：（m+2）x+（1-2m）y+4m-2=0与圆C：x²-2x+y²=0交于M，N两点．
  （1）求l的斜率的取值范围．
  （2）若O为坐标原点，直线OM与ON的斜率分别为k₁，k₂，试问k₁+k₂是否为定值？若是求出该定值；若不是，请说明理由．
  组卷：195引用：4难度：0.8

  解析

• 22．已知圆C经过（-2，3），（4，3），（1，0）三点．
  （1）求圆C的方程；
  （2）设点A在圆C上运动，点B（7，6），且点M满足

  AM

  =2

  MB

  ，记点M的轨迹为Γ．
  ①求Γ的方程；
  ②试探究：在直线l：y=x上是否存在定点T（异于原点O），使得对于Γ上任意一点P，都有

  |

  PO

  |

  |

  PT

  |

  为一常数，若存在，求出所有满足条件的点T的坐标，若不存在，说明理由．
  组卷：647引用：6难度：0.5

  解析