2023-2024学年北京166中高二（上）期中数学试卷

一、选择题（本大题共10小题，每小题4分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．直线x+y-

  3

  =0的倾斜角为（　　）

  A．45°

  B．60°

  C．120°

  D．135°
  组卷：266引用：7难度：0.9

  解析

• 2．在三棱柱ABC-A₁B₁C中，M，N分别为A₁C₁，B₁B的中点，若

  MN

  =

  x

  AB

  +

  y

  AC

  +

  z

  A

  A

  1

  ，则（x,y,z）=（　　）

  A．（1，- 1 2 ，- 1 2 ）	B．（1， 1 2 ，- 1 2 ）
  C．（-1， 1 2 ， 1 2 ）	D．（-1， 1 2 ，- 1 2 ）
  组卷：279引用：5难度：0.8

  解析

• 3．设A（2，-1），B（4，1），则以线段AB为直径的圆的方程是（　　）

  A．（x-3）2+y2=2	B．（x-3）2+y2=8
  C．（x+3）2+y2=2	D．（x+3）2+y2=8
  组卷：1974引用：12难度：0.9

  解析

• 4．《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著．某中学为了解本校学生阅读四大名著的情况，随机调查了100位学生，其中阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《红楼梦》的学生共有80位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，则该校阅读过《西游记》的学生人数与该学校学生总数比值的估计值为（　　）

  A．0.5

  B．0.6

  C．0.7

  D．0.8
  组卷：5033引用：19难度：0.6

  解析

• 5．设λ∈R，则“λ=1”是“直线3x+（λ-1）y=1与直线λx+（1-λ）y=2平行”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：258引用：11难度：0.7

  解析

• 6．投篮测试中，每人投3次，至少投中2次才能通过测试．已知某同学每次投篮投中的概率为0.6，且各次投篮是否投中相互独立，则该同学通过测试的概率为（　　）

  A．0.648

  B．0.432

  C．0.36

  D．0.312
  组卷：6617引用：47难度：0.9

  解析

• 7．埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（　　）

  A． 5 - 1 4

  B． 5 + 1 4

  C． 5 + 1 2

  D． 5 - 1 2
  组卷：1391引用：13难度：0.7

  解析

三、解答题（本大题共6小题，解答应写出文字说明，证明过程或演算步骤）

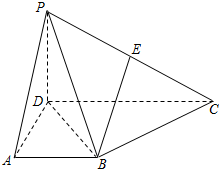• 20．在四棱锥P-ABCD中，侧面PCD⊥底面ABCD，PD⊥CD，E为PC中点，底面ABCD是直角梯形，AB∥CD，∠ADC=90°，AB=AD=PD=1，CD=2．
  （Ⅰ）求证：BE∥平面PAD；
  （Ⅱ）求证：BC⊥平面PBD；
  （Ⅲ）在线段PC上是否存在一点Q，使得二面角Q-BD-P为45°？若存在，求

  |

  PQ

  |

  |

  PC

  |

  的值；若不存在，请述明理由．
  组卷：104引用：4难度：0.5

  解析

• 21．设n为正整数，集合A={α|α=（t₁，t₂，…t_n），t_k∈{0，1}，k=1，2，…，n}，对于集合A中的任意元素α=（x₁，x₂，…，x_n）和β=（y₁，y₂，…y_n），记M（α，β）=

  1

  2

  [（x₁+y₁-|x₁-y₁|）+（x₂+y₂-|x₂-y₂|）+…（x_n+y_n-|x_n-y_n|）]．
  （Ⅰ）当n=3时，若α=（1，1，0），β=（0，1，1），求M（α，α）和M（α，β）的值；
  （Ⅱ）当n=4时，设B是A的子集，且满足：对于B中的任意元素α，β，当α，β相同时，M（α，β）是奇数；当α，β不同时，M（α，β）是偶数．求集合B中元素个数的最大值；
  （Ⅲ）给定不小于2的n,设B是A的子集，且满足：对于B中的任意两个不同的元素α，β，M（α，β）=0，写出一个集合B，使其元素个数最多，并说明理由．
  组卷：1441引用：21难度：0.1

  解析