2023-2024学年重庆八中高二（上）第一次月考数学试卷

一、选择题：本题共8小题，每小题5分，共计40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

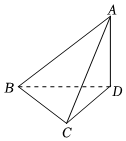• 1．在三棱锥A-BCD中，若AD⊥BC，AD⊥BD，那么必有（　　）

  A．平面ADC⊥平面BCD	B．平面ABC⊥平面BCD
  C．平面ABD⊥平面ADC	D．平面ABD⊥平面ABC
  组卷：1017引用：7难度：0.5

  解析

• 2．若过点P（0，-1）的直线l与圆

  （

  x

  -

  3

  ）

  2

  +

  y

  2

  =

  1

  有公共点，则直线l的倾斜角的最大值（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  组卷：305引用：3难度：0.6

  解析

• 3．在平面直角坐标系中，矩形OABC，O（0，0），A（2，0），C（0，1），将矩形折叠，使O点落在线段BC上，设折痕所在直线的斜率为k,则k的取值范围为（　　）

  A．[0，1]

  B．[0，2]

  C．[-1，0]

  D．[-2，0]
  组卷：180引用：8难度：0.9

  解析

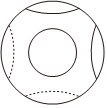• 4．某同学在参加《通用技术》实践课时，制作了一个工艺品，如图所示，该工艺品可以看成是一个球被一个棱长为

  4

  3

  的正方体的六个面所截后剩余的部分（球心与正方体的中心重合），若其中一个截面圆的周长为4π，则该球的体积是（　　）

  A． 256 π 3

  B．64π

  C．16π

  D． 32 π 3
  组卷：445引用：4难度：0.8

  解析

• 5．已知椭圆C：

  x

  2

  25

  +

  y

  2

  9

  =

  1

  的左、右焦点分别为F₁，F₂，点M在椭圆C上，当△MF₁F₂的面积最大时，△MF₁F₂内切圆半径为（　　）

  A．3

  B．2

  C． 5 3

  D． 4 3
  组卷：671引用：8难度：0.6

  解析

• 6．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的焦距为6，过右焦点F的直线l交椭圆C于A，B两点，若AB中点坐标为（1，-1），则C的方程为（　　）

  A． x 2 45 + y 2 36 = 1	B． x 2 18 + y 2 9 = 1
  C． x 2 45 + y 2 9 = 1	D． x 2 72 + y 2 36 = 1
  组卷：684引用：5难度：0.5

  解析

• 7．已知F₁，F₂是椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦点，A是C的左顶点，点P在过A且斜率为

  3

  6

  的直线上，△PF₁F₂为等腰三角形，∠F₁F₂P=120°，则C的离心率为（　　）

  A． 2 3

  B． 1 2

  C． 1 3

  D． 1 4
  组卷：15888引用：62难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．过点M（1，0）的直线l与圆C：x²+（y-2）²=4交于A，B两点．N为圆C与y轴正半轴的交点．
  （I）若|AB|=2

  3

  ，求直线l的方程：
  （II）证明：直线AN，BN的斜率之和为定值．
  组卷：281引用：4难度：0.3

  解析

• 22．已知点（-2，0）在椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  上，设点A，B为C的短轴的上、下顶点，点T是椭圆上任意一点，且TA，TB的斜率之积为-

  3

  4

  ．
  （1）求C的方程；
  （2）过C的两焦点F₁、F₂作两条相互平行的直线l₁，l₂交C于M，N和P，Q，求四边形PQNM面积的取值范围．
  组卷：148引用：5难度：0.4

  解析