2022-2023学年福建省福州二中高一（下）期末数学试卷

一、单选题（本大题共8小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．若复数z满足z（1+i）=2i,则|z|等于（　　）

  A．1

  B． 2

  C． 3

  D．2
  组卷：63引用：8难度：0.9

  解析

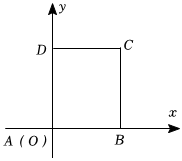• 2．如图，在矩形ABCD中，AB=2，AD=3，用斜二测画法画出的水平放置的矩形ABCD的直观图为四边形A'B'C'D'，则四边形A'B'C'D'的周长为（　　）

  A．10

  B．8

  C．7

  D．5
  组卷：119引用：5难度：0.8

  解析

• 3．抛掷两枚均匀的硬币，出现两枚正面朝上的概率等于（　　）

  A． 1 8

  B． 1 4

  C． 3 8

  D． 1 2
  组卷：18引用：4难度：0.7

  解析

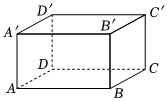• 4．在长方体ABCD-A'B'C'D'中，AB=

  3

  ，AD=

  3

  ，AA′=1，则AA′和BC′所成的角是（　　）

  A．60°

  B．45°

  C．30°

  D．90°
  组卷：51引用：5难度：0.9

  解析

• 5．△ABC中，

  AD

  =

  1

  3

  AB

  ，点E是CD的中点，设

  AB

  =

  a

  ，

  AC

  =

  b

  ，则

  AE

  =（　　）

  A． 1 2 a + 1 6 b

  B． 1 6 a + 2 3 b

  C． 1 2 a + 1 3 b

  D． 1 6 a + 1 2 b
  组卷：258引用：11难度：0.7

  解析

• 6．如图，点A，B，C，M，N为正方体的顶点或所在棱的中点，则下列各图中，不满足直线MN∥平面ABC的是（　　）

  A．

  B．

  C．

  D．
  组卷：660引用：10难度：0.6

  解析

• 7．投掷一枚均匀的骰子，记事件A：“朝上的点数大于3”，B：“朝上的点数为2或4”，则下列说法正确的是（　　）

  A．事件A与事件B互斥	B．事件A与事件B对立
  C．事件A与事件B相互独立	D． P （ A + B ） = 5 6
  组卷：287引用：4难度：0.7

  解析

四、解答题：（本题共6小题，共70=10+12×5分.解答应写出文字说明、证明过程或演算步骤）

• 21．已知向量

  a

  =

  （

  cos

  （

  π

  2

  -

  θ

  ）

  ，

  sin

  （

  π

  2

  -

  θ

  ）

  ）

  ，

  b

  =

  （

  cosθ

  ，-

  sinθ

  ）

  ．
  （1）求

  |

  a

  |

  ，

  |

  b

  |

  和

  a

  •

  b

  的值；
  （2）令

  m

  =

  （

  t

  2

  +

  4

  ）

  a

  +

  b

  ，

  n

  =

  t

  a

  -

  k

  b

  ，若存在正实数k和t,使得

  m

  ⊥

  n

  ，求此时

  k

  t

  2

  的最小值．
  组卷：63引用：3难度：0.7

  解析

• 22．如图，在四棱锥P-ABCD中，底面ABCD为矩形，△PAD是边长为2的正三角形，平面PAD⊥平面ABCD，E为棱PD的中点．
  （1）求证：AE⊥平面PCD；
  （2）若直线PC与平面ABCD所成角的正切值为

  3

  2

  ，求侧面PAD与侧面PBC所成二面角的大小．
  组卷：180引用：3难度：0.6

  解析