2022-2023学年河南省南阳市六校高一（下）第一次联考数学试卷

一、选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．下列角中，与角1560°终边相同的角是（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 4 π 3
  组卷：85引用：3难度：0.7

  解析

• 2．在函数①y=sin|2x|，②y=|cosx|，③

  y

  =

  cos

  （

  2

  x

  +

  π

  6

  ）

  ，④

  y

  =

  tan

  （

  2

  x

  -

  π

  4

  ）

  中，最小正周期为π的所有函数为（　　）

  A．②③

  B．①③④

  C．②④

  D．①③
  组卷：95引用：1难度：0.7

  解析

• 3．要得到

  y

  =

  sin

  x

  2

  的图象，只需将函数

  y

  =

  cos

  （

  x

  2

  -

  π

  4

  ）

  的图象（　　）

  A．向左平移 π 4 个单位长度	B．向右平移 π 4 个单位长度
  C．向左平移 π 2 个单位长度	D．向右平移 π 2 个单位长度
  组卷：390引用：4难度：0.7

  解析

• 4．函数

  f

  （

  x

  ）

  =

  1

  -

  sinx

  3

  sinx

  +

  2

  的值域为（　　）

  A．（-∞，-2）∪（0，+∞）	B．（-∞，-2]∪[0，+∞）
  C．（-∞，-2）∪[0，+∞）	D．（-∞，-2]∪（0，+∞）
  组卷：65引用：2难度：0.7

  解析

• 5．在直径为4cm的圆中，72°的圆心角所对的弧长是（　　）

  A． 4 π 5 cm

  B． 2 π 5 cm

  C． π 3 cm

  D． π 2 cm
  组卷：215引用：3难度：0.8

  解析

• 6．△ABC中角C为钝角，若角θ终边上一点P的坐标为（sinA-cosB，cosA-sinB），则

  y

  =

  sinθ

  |

  sinθ

  |

  +

  |

  cosθ

  |

  cosθ

  +

  tanθ

  |

  tanθ

  |

  的值为（　　）

  A．1

  B．-1

  C．2

  D．-2
  组卷：22引用：2难度：0.7

  解析

• 7．若函数f（x）=sinωx（ω＞0）在区间

  [

  π

  2

  ，

  2

  π

  3

  ]

  上单调递减，且f（x）=1在区间[0，2π]上有唯一的实数解，则ω的取值范围是（　　）

  A． [ 1 4 ， 3 ]

  B． [ 3 2 ， 5 4 ]

  C． [ 1 ， 5 4 ）

  D． [ 3 2 ， 3 ]
  组卷：251引用：2难度：0.6

  解析

四、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）

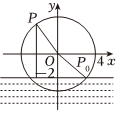• 21．直径为8m的水轮如图所示，水轮圆心O距离水面2m,已知水轮沿逆时针方向匀速旋转，每分钟转动6圈，当水轮上点P从水中浮现时（图中点P₀）开始计算时间．
  （1）将点P距离水面的高度h（m）表示为时间t（s）的函数；
  （2）在水轮转动的一圈内，有多长时间点P在水面下？
  组卷：40引用：2难度：0.6

  解析

• 22．已知奇函数f（x）的定义域为实数集R，且f（x）在（-∞，+∞）上是减函数，是否存在这样的实数m,使f（4m-2mcosθ）+f（2cos²θ-4）＞f（0）对所有的

  θ

  ∈

  [

  -

  π

  3

  ，

  π

  2

  ]

  均成立？若存在，求出适合条件的实数m的取值范围；若不存在，说明理由．
  组卷：4引用：2难度：0.5

  解析