2023年湖北省襄阳市老河口市中考数学联考试卷(4月份)
发布:2024/8/31 0:0:8
一、选择题(本大题共10个小题,每小题3分,共30分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将其序号在答题卡上涂黑作答.
-
1.下列四个数中,最大的数是( )
组卷:33引用:1难度:0.7 -
2.下列运算正确的是( )
组卷:48引用:12难度:0.9 -
 3.如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( )组卷:836引用:5难度:0.8
3.如图,已知AB∥CD,DE⊥AC,垂足为E,∠A=120°,则∠D的度数为( )组卷:836引用:5难度:0.8 -
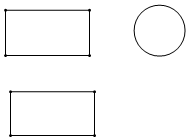 4.如图是某几何体的三视图,该几何体是( )组卷:323引用:7难度:0.9
4.如图是某几何体的三视图,该几何体是( )组卷:323引用:7难度:0.9 -
5.不等式组
的解集在数轴上表示为( )2x-2≤0x>-1组卷:567引用:7难度:0.8 -
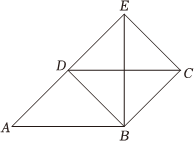 6.如图,延长▱ABCD的边AD到E,使DE=AD,连接BE,DB,EC.再添加一个条件,不能使四边形BCED成为矩形的是( )组卷:530引用:4难度:0.5
6.如图,延长▱ABCD的边AD到E,使DE=AD,连接BE,DB,EC.再添加一个条件,不能使四边形BCED成为矩形的是( )组卷:530引用:4难度:0.5 -
7.下列说法正确的是( )
组卷:154引用:6难度:0.6 -
8.有一人患了流行性感冒,经过两轮传染后共有121个人患了流行性感冒,设每轮传染中平均一个人传染了x个人,则根据题意可列方程为( )
组卷:421引用:2难度:0.6
三、解答题(本大题共9个小题,共72分)解答应写出文字说明,证明过程或演算步骤,并且写在答题卡上每题对应的答题区域内.
-
24.几何综合:
已知:点D是△BAC边BC上一动点,作△DAE∽△BAC,点M、点N分别是边AB、AC的中点,连接MD、NE;设=k(常数k>0).ACAB
(1)证明推断:
若k=1.如图①,当∠BAC=∠DAE=60°时,
①求证:△DAM≌△EAN;
②推断:当MD⊥BC时,=;NECN
(2)类比探究:
若k≠1.如图②,当MD⊥BC时,试写出线段DB2、EN2、CN2与常数k之间一个相等关系,并证明;
(3)拓展应用:
若k≠1.如图③,设∠BAC=∠DAE=90°,MD⊥BC,当NE=4,DB=时,求常数k的值和线段DA的长度.94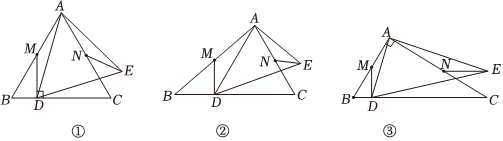 组卷:273引用:1难度:0.5
组卷:273引用:1难度:0.5 -
25.坐标综合:
(1)平面直角坐标系中,抛物线C1:y1=x2+bx+c的对称轴为直线x=3,且经过点(6,3),求抛物线C1的解析式,并写出其顶点坐标;
(2)将抛物线C1在平面直角坐标系内作某种平移,得到一条新的抛物线C2:y2=x2-2mx+m2-1,
①如图1,设自变量x在1≤x≤2的范围内取值时,函数y2的最小值始终等于-1.此时,若y2的最大值比最小值大,求m的值;12m
②如图2,直线l:y=x+n(n>0)与x轴、y轴分别交于A、C两点.过点A、点C分别作两坐标轴的平行线,两平行线在第一象限内交于点B.设抛物线C2与x轴交于E、F两点(点E在左边).现将图中的△CBA沿直线l折叠,折叠后的BC边与x轴交于点M.当8≤n≤12时,若要使点M始终能够落在线段EF(包括两端点)上,请通过计算加以说明:抛物线C1在向抛物线C2平移时,沿x轴的方向上需要向左还是向右平移?最少要平移几个单位?最多能平移几个单位?-12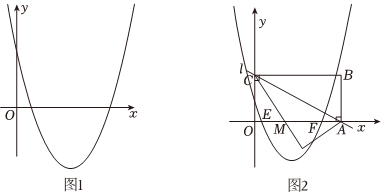 组卷:134引用:1难度:0.2
组卷:134引用:1难度:0.2


