2023-2024学年上海市奉贤中学高二（上）月考数学试卷（10月份）

一、填空题（本大题共有12小题，满分54分，第1-6题每题4分，第7-12题每题5分）

• 1．已知点A（0，0），B（2，3），则直线AB的倾斜角α=

  ．
  组卷：26引用：2难度：0.8

  解析

• 2．已知向量

  a

  =

  （

  -

  3

  ，

  2

  ，

  4

  ）

  ，

  b

  =

  （

  1

  ，-

  2

  ，

  2

  ）

  ，则

  |

  a

  -

  b

  |

  =

  ．
  组卷：33引用：2难度：0.5

  解析

• 3．过点（-2，3）且与直线2x+y+1=0垂直的直线l的方程是

  ．
  组卷：140引用：6难度：0.8

  解析

• 4．已知向量

  a

  =

  （

  2

  ，

  1

  ，

  3

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ，-

  1

  ）

  ，

  c

  =

  （

  4

  ，

  3

  ，

  m

  ）

  ，若

  a

  ，

  b

  ，

  c

  共面，则m=

  ．
  组卷：60引用：3难度：0.5

  解析

• 5．若直线l₁：3kx-（k+2）y+6=0和直线l₂：kx+（2k-3）y+2=0斜率互为相反数，则k=

  ．
  组卷：51引用：1难度：0.8

  解析

• 6．点

  A

  （

  3

  2

  ，

  2

  ）

  关于直线

  x

  +

  y

  +

  1

  3

  =

  0

  的对称点为

  ．
  组卷：96引用：2难度：0.6

  解析

• 7．已知平面α的一个法向量为

  n

  =

  （

  1

  ，-

  1

  ，

  1

  ）

  ，直线l的一个方向向量为

  m

  =

  （

  2

  ，

  2

  ，

  0

  ）

  ，则直线l与平面α的位置关系是

  ．
  组卷：29引用：1难度：0.8

  解析

三、解答题（本大题共5题，满分78分）

• 20．已知直线l：ax-y+2-a=0恒过点P，且与x轴，y轴分别交于A，B两点，O为坐标原点．
  （1）求点P的坐标；
  （2）当点O到直线l的距离最大时，求直线l的方程；
  （3）当|PA|•|PB|取得最小值时，求△AOB的面积．
  组卷：395引用：9难度：0.7

  解析

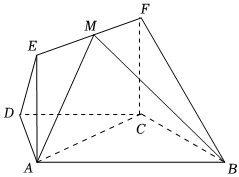• 21．如图，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．
  （1）求证：BC⊥平面ACFE；
  （2）求平面ABF与平面BCF所成角的大小；
  （3）若点M在线段EF上运动，设平面MAB与平面FCB所成二面角的平面角为θ（θ≤90°），试求cosθ的范围．
  组卷：50引用：1难度：0.4

  解析