2022-2023学年江苏省宿迁市泗阳县高二（下）期中数学试卷
发布：2024/6/28 8:0:9
一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
-
1．
=（ ）5A25+4C24组卷：215引用：1难度：0.9 -
2．（2x-1）5展开式中x3的系数为（ ）
组卷：208引用：4难度：0.8 -
3．已知空间向量
=（-1，m,2），a=（-1，2，-1），若b=-3，则a•b与a的夹角为（ ）b组卷：576引用：3难度：0.7 -
4．2023年3月5号是毛泽东主席提出“向雷锋同志学习”60周年纪念日，某志愿者服务队在该日安排4位志愿者到两所敬老院开展志愿服务活动，要求每所敬老院至少安排1人，每个志愿者都要参加活动，则不同的分配方法数是（ ）
组卷：28引用：1难度：0.9 -
5．已知直线l过定点A（1，2，3），向量
=（1，0，1）为其一个方向向量，则点P（4，3，2）到直线l的距离为（ ）n组卷：300引用：8难度：0.5 -
6．将三枚骰子各掷一次，设事件A为“三个点数都不相同”，事件B为“出现一个6点”，则概率P（B|A）的值为（ ）
组卷：35引用：1难度：0.8 -
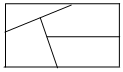7．用6种不同的颜色给如图所示的地图上色，要求相邻两块涂不同的颜色，则不同的涂色方法有（ ）组卷：396引用：12难度：0.9
四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。
-
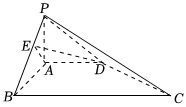21．如图，四棱锥P-ABCD的底面ABCD是梯形，PA⊥平面ABCD，AD∥BC，AB=AP=2，BC=2AD=，∠ABC=45°，E为线段PB上一个动点．22
（1）若E为线段PB的中点，求E到平面PDC的距离；
（2）求直线PC与平面EAD所成角的正弦值的最大值．
组卷：91引用：4难度：0.6 -
22．在（x2+x+1）n=
D0nx2n+D1nx2n-1+D2nx2n-2的展开式中，把+…+D2n-1nx+D2nn，D0n，D1n叫做三项式的n次系数列．D2n，⋯，D2nn
（1）求的值；D03+D23+D43+D63
（2）根据二项式定理，将等式（1+x）2n=（1+x）n（1+x）n的两边分别展开，可得左右两边的系数对应相等，如，利用上述思想方法，求Cn2n=（C0n）2+（C1n）2+（c2n）2+⋯+（Cnn）2D02023C02023-D12023C12023+D22023C22023-…-的值．D20212023C20212023+D20222023C20222023-D20232023C20232023组卷：58引用：3难度：0.4
