2023年甘肃省定西市中考数学二模试卷

一、选择题：本大题共10个小题，每小题3分，共30分，每小题只有一个正确选项

• 1．下列二次根式中，是最简二次根式的是（　　）

  A． 1 2

  B． 11

  C． 27

  D． a 3
  组卷：1639引用：14难度：0.8

  解析

• 2．下列设计图中，是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：8引用：3难度：0.8

  解析

• 3．在平面直角坐标系中，点P（-2，x²+1）所在的象限是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：13225引用：100难度：0.9

  解析

• 4．一元一次不等式组

  2 x + 1 ＞ 0

  x - 5 ≤ 0

  的解集中，整数解的个数是（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：599引用：60难度：0.9

  解析

• 5．如图，数轴上的点A，B，O，C，D分别表示数-2，-1，0，1，2，则表示数2-

  5

  的点P应落在（　　）

  A．线段AB上

  B．线段BO上

  C．线段OC上

  D．线段CD上
  组卷：2239引用：23难度：0.7

  解析

• 6．下列命题是真命题的是（　　）

  A．中位数就是一组数据中最中间的一个数

  B．一组数据的众数可以不唯一

  C．已知a、b、c是Rt△ABC的三条边，则a2+b2=c2

  D．邻边相等的平行四边形是矩形
  组卷：36引用：6难度：0.5

  解析

• 7．若单项式2x²y^a+b与3x^a-by⁴是同类项，则a,b的值分别是（　　）

  A．a=3，b=1

  B．a=-3，b=1

  C．a=3，b=-1

  D．a=-3，b=-1
  组卷：721引用：9难度：0.9

  解析

• 8．如图，有一张直角三角形纸片ABC，两条直角边AC=5，BC=10，将△ABC折叠，使点A和点B重合，折痕为DE，则CD的长为（　　）

  A．1.8

  B．2.5

  C．3

  D．3.75
  组卷：688引用：7难度：0.5

  解析

• 9．如图，A、B、C是圆O上的三点，且四边形ABCO是平行四边形，OF⊥OC交圆O于点F，∠AOF等于（　　）

  A．15°

  B．30°

  C．45°

  D．60°
  组卷：99引用：1难度：0.5

  解析

四、解答题（二）；本大题共5小题，共40分，解答应写出必要的文字说明，证明过程或演算步骤

• 27．（1）建立模型：如图1，在正方形ABCD中，E，F分别是BC，CD上的点，且∠EAF=45°，探究图中线段BE，EF，FD之间的数量关系．小王同学探究此问题的方法是将△ABE绕A点逆时针旋转90°使得B与D重合，连接AG，由此得到BE=

  ，再证明△AFE≌△

  ，可得出线段BE，EF，FD之间的数量关系为

  ．
  （2）拓展延伸：如图2，在等腰直角三角形ABC中，∠ABC=90°，AB=BC，点G，H在边AC上，且∠GBH=45°，写出图中线段AG，GH，CH之间的数量关系并证明．
  
  组卷：88引用：6难度：0.5

  解析

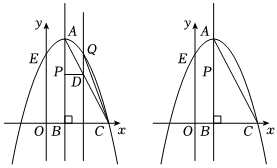• 28．如图，在平面直角坐标系中，Rt△ABC的边BC在x轴上，∠ABC=90°，以A为顶点的抛物线y=-x²+bx+c经过点C（3，0），交y轴于点E（0，3），动点P在对称轴上．
  ​（1）求抛物线的解析式．
  （2）若点P从A点出发，沿A→B方向以1个单位长度/秒的速度匀速运动到点B停止，设运动时间为t秒，过点P作PD⊥AB交AC于点D，过点D且平行于y轴的直线l交抛物线于点Q，连接AQ，CQ，当t为何值时，△ACQ的面积最大？最大值是多少？
  （3）抛物线上是否存在点M，使得以点P，M，E，C为顶点的四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由．
  组卷：131引用：7难度：0.5

  解析