2023-2024学年上海实验学校高三（上）开学数学试卷（暑假反馈）
发布：2024/8/2 8:0:9
一、填空题（第1-6题每题4分，第7-12题每题5分，满分54分）
-
1．不等式
的解集为 ．3x＜1组卷：51引用：5难度：0.8 -
2．已知
，则sinx=-13，tanx＞0=．sin（π2+x）组卷：57引用：2难度：0.8 -
3．若
，其中i是虚数单位，则z+z2+z3+⋯+z2022=．z=1+i1-i组卷：54引用：2难度：0.7 -
4．一个圆锥的侧面展开图是圆心角为
的扇形，则其母线与底面所成角的余弦值为 ．4π3组卷：93引用：2难度：0.7 -
5．曲线
在点（1，f（1））处的切线与坐标轴围成的三角形面积为 ．f（x）=xx-2组卷：57引用：2难度：0.7 -
6．已知数列{bn}的前n项和为
，则{bn}的通项公式bn=．Sn=23bn+13组卷：62引用：2难度：0.5 -
7．已知
，则P（A）=0.4，P（B|A）=0.2，P（B|A）=0.3=．P（B）组卷：121引用：3难度：0.7
三、解答题（本大题共有5题，满分76分）
-
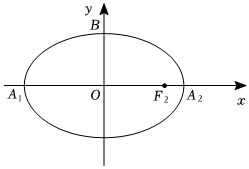20．设A1、A2分别是椭圆的左、右顶点，点B为椭圆的上顶点．Γ：x2a2+y2=1（a＞1）
（1）若Γ的离心率为，求Γ的方程；63
（2）设是Γ的右焦点，点Q是Γ上的任意动点（不在直线BF上），求△QBF2的面积S的最大值；a=2，F2
（3）设a=3，点P是直线x=6上的动点，点C和D是Γ上异于左、右顶点的两点，且C、D分别在直线PA1和PA2上，求证：直线CD恒过一定点．组卷：52引用：1难度：0.5 -
21．已知函数g（x）=3x，h（x）=[g（x）]2．
（1）解方程：x+log3[2g（x）-8]=log3[h（x）+9]；
（2）令，求证：p（x）=g（x）g（x）+3，q（x）=3h（x）+3p（32022）+p（42022）+⋯+p（20182022）+；p（20192022）=q（32022）+q（42022）+⋯+q（20182022）+q（20192022）
（3）若是R上的奇函数，且f[h（x）-1]+f[2-k•g（x）]＞0对任意实数x恒成立，求实数k的取值范围．f（x）=g（x+1）+ag（x）+b组卷：25引用：2难度：0.5
