2022-2023学年湖北省恩施州高中教育联盟高一(下)期末数学试卷
发布:2024/6/28 8:0:9
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.已知i为虚数单位,复数z=i(3+3i),则其共轭复数的虚部是( )
组卷:21引用:2难度:0.8 -
2.已知向量
满足a,b,|a|=2,|b|=1,则cos〈a,b〉=14在b上的投影向量为( )a组卷:54引用:2难度:0.7 -
3.已知函数f(x)=max{x2,5x-6},则下列说法正确的是( )
组卷:152引用:2难度:0.7 -
4.数学家纳皮尔发明了对数,对数的思想方法是把乘方和乘法运算分别转化为乘法和加法运算.已知lg2≈0.3010,lg3≈0.4771,设N=810×95,则N所在的区间为( )
组卷:72引用:2难度:0.7 -
 5.函数的部分图象如图所示,则( )y=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)组卷:95引用:2难度:0.7
5.函数的部分图象如图所示,则( )y=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)组卷:95引用:2难度:0.7 -
6.已知α,β是两个不同的平面,m,n是两条不同的直线,则下列命题中不正确的是( )
组卷:140引用:9难度:0.7 -
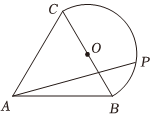 7.如图所示,边长为1的正△ABC,以BC的中点O为圆心,BC为直径在点A的另一侧作半圆弧,点P在圆弧上运动,则ˆBC的取值范围( )AB•AP组卷:58引用:2难度:0.6
7.如图所示,边长为1的正△ABC,以BC的中点O为圆心,BC为直径在点A的另一侧作半圆弧,点P在圆弧上运动,则ˆBC的取值范围( )AB•AP组卷:58引用:2难度:0.6
四、解答题:本题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
-
 21.如图,四棱锥S-ABCD中,底面ABCD为菱形,∠ABC=60°,SA=AB=SD=2,侧面SAB⊥侧面SBC,M为AD的中点.
21.如图,四棱锥S-ABCD中,底面ABCD为菱形,∠ABC=60°,SA=AB=SD=2,侧面SAB⊥侧面SBC,M为AD的中点.
(1)求证:平面SMC⊥平面SBC;
(2)若AB与平面SBC成30°角时,求二面角A-SC-D的大小.组卷:278引用:5难度:0.6 -
22.已知
,ω>0,且函数a=(sinωx,cosωx),b=(cosωx,3cosωx).现将绘有函数f(x)的一个周期图象(含有最高点和最低点)的A4纸片沿原图象上的x轴折成互相垂直的两个半平面,折叠后若原图象上的最高点和最低点此时的空间距离为f(x)=a•(b-32a).π2+82
(1)求函数f(x)的对称中心;
(2)若关于x的不等式在f(x-π6)>2msin(x+π4)-2cos(x-π4)内恒成立,求实数m的取值范围.[0,π2]组卷:17引用:2难度:0.5


