2022-2023学年湖北省武汉市江岸区高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．

  5

  （

  1

  +

  i

  3

  ）

  （

  2

  +

  i

  ）

  （

  2

  -

  i

  ）

  =（　　）

  A．-1

  B．1

  C．1-i

  D．1+i
  组卷：2158引用：8难度：0.7

  解析

• 2．一组数据按从小到大的顺序排列为1、2、4、4、4、x、7、8、8、9，若该组数据的中位数是众数的

  5

  4

  倍，则x为（　　）

  A．4

  B．5

  C．6

  D．7
  组卷：28引用：2难度：0.9

  解析

• 3．已知向量

  a

  与

  b

  的夹角为

  5

  π

  6

  ，且

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  3

  ，则

  a

  在

  b

  方向上的投影向量是（　　）

  A． - 2 3 a

  B． - 3 3 b

  C． 1 3 b

  D． - 1 3 b
  组卷：70引用：1难度：0.7

  解析

• 4．某校200名学生参加环保知识竞赛，随机抽取了20名学生的考试成组（单位：分），成绩的频率分布直方图如图所示，则下列说法正确的是（　　）

  A．频率分布直方图中a的值为0.006

  B．估计某校成绩落在[60，70）内的学生人数为50人

  C．估计这20名学生考试成绩的众数为80分

  D．估计这20名学生考试成绩的第60百分位数为80分
  组卷：135引用：3难度：0.7

  解析

• 5．已知m,n,l是三条不同的直线，α，β，γ是三个不重合的平面，则下列说法正确的是（　　）

  A．α⊥γ，β⊥γ，α∩β=l,则l⊥γ

  B．m与n异面，l⊥m,l⊥n,则不存在α，使得l⊥α，m∥α，n∥α

  C．m∥α，n∥β，α⊥β，则m⊥n

  D．m⊥α，m⊥β，n⊥α，则n∥β
  组卷：79引用：3难度：0.7

  解析

• 6．在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E、F分别是棱BC、CC₁的中点，P是侧面BCC₁B₁（包含边界）上的一动点，若A₁P∥平面AEF，则线段A₁P长度的取值范围是（　　）

  A． [ 1 ， 5 2 ]

  B． [ 3 2 4 ， 5 2 ]

  C． [ 3 2 2 ， 5 ]

  D． [ 2 ， 5 ]
  组卷：59引用：2难度：0.6

  解析

• 7．已知△ABC，AB=6，AC=4，N是边BC上的点，且

  BN

  =

  3

  NC

  ，

  O

  为△ABC的外心，则

  AN

  •

  AO

  的值为（　　）

  A． 21 2

  B．10

  C． 17 3

  D．9
  组卷：203引用：3难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

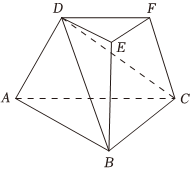• 21．如图，在三棱台ABC-DEF中，平面ACFD⊥平面ABC，∠ACB=∠ACD=45°，DC=2BC．
  （1）求异面直线EF与DB所成角的余弦值；
  （2）求二面角A-CD-B的大小的正切值．
  组卷：149引用：1难度：0.6

  解析

• 22．小明对圆柱中的截面进行一番探究．他发现用平行于底面的平面α去截圆柱可得一圆面，用与水平面成一定夹角φ的平面β去截可得一椭圆面，用过轴的平面去截可得一矩形面．
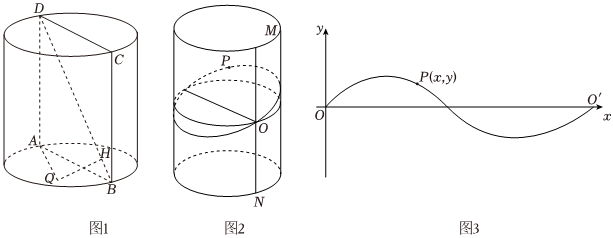
  （1）图1中，圆柱底面半径为

  3

  ，高为2，轴截面为ABCD，设Q为底面（包括边界）上一动点，满足Q到A的距离等于Q到直线DB的距离QH，求三棱锥Q-ABD体积的最大值；
  （2）如图2，过圆柱侧面上某一定点O的水平面α与侧面交成为圆C₁，过O点与水平面成φ角的平面β与侧面交成为椭圆C₂，小明沿着过O的母线MN前开，把圆柱侧面展到一个平面上，发现圆C₁展开后得到线段OO'，椭圆C₂展开后得到一正弦曲线（如图3），设P为椭圆上任意一点，他很想知道原因，于是他以O为原点，OO'为x轴建立了平面直角坐标系，且设P（x,y）（图3）．试说明为什么椭圆C₂展开后是正弦曲线，并写出其函数解析式y=f（x）．
  组卷：82引用：2难度：0.3

  解析