2022-2023学年北京市101中学高一（下）期中数学试卷

一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.

• 1．sin（-150°）的值为（　　）

  A．- 1 2

  B． 1 2

  C．- 3 2

  D． 3 2
  组卷：309引用：20难度：0.9

  解析

• 2．已知tanα=

  1

  3

  ，则tan2α=（　　）

  A．- 4 3

  B． 4 3

  C．- 3 4

  D． 3 4
  组卷：150引用：4难度：0.9

  解析

• 3．已知向量

  a

  =（1，-2），

  b

  =（x,4），且

  a

  ∥

  b

  ，则|

  a

  -

  b

  |=（　　）

  A． 5 3

  B． 3 5

  C． 2 5

  D． 2 2
  组卷：178引用：12难度：0.9

  解析

• 4．下列函数中最小正周期为π的是（　　）
  ①f（x）=cosx•sinx；
  ②f（x）=cosx+sinx；
  ③

  f

  （

  x

  ）

  =

  sinx

  cosx

  ；
  ④f（x）=2sin²x

  A．①②

  B．②④

  C．①③④

  D．①②④
  组卷：200引用：3难度：0.8

  解析

• 5．在正方形ABCD中，E为AB的中点，F为CE的中点，则

  AF

  =（　　）

  A． 3 4 AB + 1 4 AD

  B． 1 4 AB + 3 4 AD

  C． 1 2 AB + AD

  D． 3 4 AB + 1 2 AD
  组卷：411引用：8难度：0.7

  解析

• 6．在△ABC中，角A，B，C所对的边分别是a,b,c,已知a=2bcosC，则△ABC的形状是（　　）

  A．等腰三角形	B．直角三角形
  C．等腰直角三角形	D．等腰或直角三角形
  组卷：392引用：15难度：0.9

  解析

三、解答题：共5小题，共55分.解答应写出文字说明、演算步骤或证明过程.

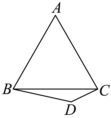• 19．在△ABC中，角A，B，C的对边分别为a,b,c,

  3

  a

  =

  b

  （

  sin

  C

  +

  3

  cos

  C

  ）

  ．
  （1）求角B的大小；
  （2）若

  A

  =

  π

  3

  ，D为△ABC外一点，如图DB=4，CD=2，求四边形ABDC面积的最大值．
  组卷：172引用：3难度：0.6

  解析

• 20．给定正整数n≥2，设M={α|α=（t₁，t₂，…，t_n），t_k∈{0，1}，k=1，2，…，n}为n维0-1向量α的集合．对于集合M中的任意元素β=（x₁，x₂，⋯，x_n）和γ=（y₁，y₂，⋯，y_n），定义它们的内积为β•γ=x₁y₁+x₂y₂+⋯+x_ny_n．
  设A⊆M．且集合A={α_i|α_i=（t_i1，t_i2，…，t_in），i-1，2，⋯，n}，对于A中任意元素α_i，α_j，若

  α

  i

  •

  α

  j

  =

  p , i = j ,

  q , i ≠ j ,

  则称A具有性质H（p,q）．
  （1）当n=3时，判断集合A={（1，1，0），（1，0，1），（0，1，1）}是否具有性质H（2，0）？说明理由；
  （2）当n=4时，判断是否存在具有性质H（p,q）的集合A，若存在求出p,q,若不存在请证明；
  （3）若集合A具有性质H（p,1），证明：t_1j+t_2j+⋯+t_nj=p（j=1，2，⋯，n）．
  组卷：50引用：2难度：0.4

  解析