2022-2023学年广东省肇庆一中高三（上）月考数学试卷（11月份）

一、单选题（共40分）

• 1．设集合M={x|log₂x＜1}，N={x|2x-1＜0}，则M∩N=（　　）

  A．{x|x＜2}

  B． { x | x ＜ 1 2 }

  C．{x|0＜x＜2}

  D． { x | 0 ＜ x ＜ 1 2 }
  组卷：192引用：7难度：0.7

  解析

• 2．若（1-i）（1-z）=1，则z的虚部为（　　）

  A． 1 2

  B． 1 2 i

  C． - 1 2

  D． - 1 2 i
  组卷：5引用：3难度：0.8

  解析

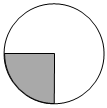• 3．如图，圆形纸片的四分之一扇形（阴影部分）是圆锥A的侧面展开图，其余部分是圆锥B的侧面展开图，则圆锥A与圆锥B的表面积之比为（　　）

  A． 9 25

  B． 5 21

  C． 1 3

  D． 9 16
  组卷：9引用：2难度：0.7

  解析

• 4．若关于x的不等式a•2^|x|＞2^|x|+1（x∈R）有实数解，则实数a的取值范围是（　　）

  A．（1，+∞）

  B．（2，+∞）

  C．[1，+∞）

  D．[2，+∞）
  组卷：9引用：2难度：0.5

  解析

• 5．已知角α满足

  tan

  （

  α

  -

  π

  4

  ）

  =

  1

  3

  ，则sin2α=（　　）

  A． 4 5

  B． - 4 5

  C． - 7 9

  D． 4 9
  组卷：199引用：5难度：0.7

  解析

• 6．“割圆术”是我国古代计算圆周率π的一种方法．在公元263年左右，由魏晋时期的数学家刘徽发明．其原理就是利用圆内接正多边形的面积逐步逼近圆的面积，进而求π．当时刘徽就是利用这种方法，把π的近似值计算到3.1415和3.1416之间，这是当时世界上对圆周率π的计算最精确的数据．这种方法的可贵之处就是利用已知的、可求的来逼近未知的、要求的，用有限的来逼近无穷的．为此，刘徽把它概括为“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”．这种方法极其重要，对后世产生了巨大影响，在欧洲，这种方法后来就演变为现在的微积分．根据“割圆术”，若用正六十边形来估算圆周率π，则π的近似值是（　　）（精确到0.001）（参考数据sin6°≈0.10452）

  A．3.136

  B．3.109

  C．3.190

  D．3.142
  组卷：3引用：3难度：0.7

  解析

• 7．若将函数

  f

  （

  x

  ）

  =

  sin

  2

  x

  -

  3

  cos

  2

  x

  的图象向右平移m（m＞0）个单位后，所得图象对应的函数为奇函数，则m的最小值是（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：20引用：3难度：0.7

  解析

四、解答题（共70分）

• 21．已知函数f（x）=ax²-（a+2）x+lnx（a＞0）．
  （1）若x=1是函数f（x）的极值点，求f（x）在区间

  [

  1

  2

  ，

  2

  ]

  上的最值；
  （2）求函数f（x）的单调增区间．
  组卷：135引用：7难度：0.6

  解析

• 22．已知函数f（x）=ae^x+ln（ea）（a＞0）．
  （1）当a=1时，求过点（-2，0）且和曲线y=f（x）相切的直线方程；
  （2）若对任意实数x＞1，不等式f（x）≥ln（x-1）恒成立，求实数a的取值范围．
  组卷：137引用：5难度：0.4

  解析