2023-2024学年浙江省台州市临海市第六教研区八年级（上）期中数学试卷
发布：2024/10/1 9:0:4
一、选择题（本大题共10小题，每小题3分，共30分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）
-
1．第19届亚运会将于2023年9月在杭州举行，下列历届亚运会会徽是轴对称图形的是（ ）
组卷：266引用：15难度：0.9 -
2．在△ABC中，作出AC边上的高，正确的是（ ）
组卷：2318引用：21难度：0.6 -
3．七年级一班计划在学校英语角里搭三角形围栏，可以选择三种长度的木条组合是（ ）
组卷：176引用：5难度：0.7 -
4．如图，图中显示的是从镜子中看到背后墙上的电子钟读数，由此你可以推断这时的实际时间是（ ）组卷：2126引用：52难度：0.9 -
5．用直尺和圆规作一个角等于已知角的示意图如图所示，由此说明△OCD≌△O′C′D′的依据是（ ）组卷：169引用：5难度：0.9 -
6．等腰三角形的周长是8cm,其中一边长为2cm,则该等腰三角形的底边长为（ ）
组卷：36引用：1难度：0.6 -
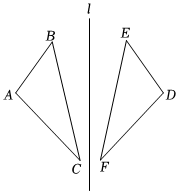7．如图所示，△ABC与△DEF关于直线l对称，下列说法错误的是（ ）组卷：70引用：4难度：0.7 -
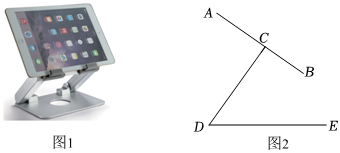8．如图1，这是一个平板电脑支架，由托板、支撑板和底座构成，平板电脑放置在托板上，图2是其侧面结构示意图．现量得托板长AB=10cm,支撑板顶端的C恰好是托板AB的中点，托板AB可绕点C转动，支撑板CD可绕点D转动．当CD⊥AB，且射线DB恰好是∠CDE的平分线时，此时点B到直线DE的距离是（ ）组卷：398引用：14难度：0.6
三、解答题（本题共8小题，第17-19题每小题0分，第20-21题每小题0分，第22-23题每小题0分，第24题12分，共66分）
-
23．已知△ABC．
（1）如图1，若三角形的内角∠ABC与∠ACB的平分线交于点O，求证：
①∠BOC=180°-（∠ABC+∠ACB）；12
②∠BOC=90°+∠A；12
（2）如图2，若三角形的外角∠DBC与∠ECB的平分线交于点O，试分析∠BOC与∠A有怎样的数量关系，请说明理由；
（3）如图3，，若三角形的内角∠ABC与外角∠ACD的平分线交于点O，则∠BOC与∠A的数量关系为 ．（只写结论，不需证明）
组卷：142引用：1难度：0.7 -
24．（1）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线l经过点A，BD⊥直线l,CE⊥直线l,垂足分别为点D、E．证明：DE=BD+CE．
（2）组员小刘想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线l上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．
（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高，延长HA交EG于点I，求证：I是EG的中点．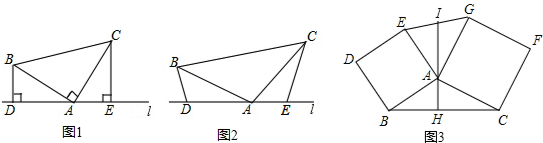
组卷：13403引用：41难度：0.3
