2022-2023学年辽宁省沈阳市联合体高一（下）期末数学试卷

一、单选题（本大题共8小题，每小题5分，共40分．在每小题所给的四个选项中，有且只有一项是符合题目要求的）

• 1．cos1560°的值为（　　）

  A． 1 2

  B． - 1 2

  C． 3 2

  D． - 3 2
  组卷：226引用：1难度：0.8

  解析

• 2．已知i为虚数单位，复数

  z

  =

  2

  -

  i

  2

  +

  i

  （

  a

  ∈

  R

  ）

  ，则它的共轭复数

  z

  为（　　）

  A． 3 5 + 4 5 i

  B． 3 5 - 4 5 i

  C． 1 + 4 5 i

  D． 1 - 4 5 i
  组卷：46引用：1难度：0.8

  解析

• 3．如图，一个水平放置的四边形ABCD的斜二测画法的直观图是矩形A′B′C′D′，O′A′=4，A′B′=3，O′是A′D′的中点，则原四边形ABCD的面积是（　　）

  A．20

  B．40

  C．80

  D．160
  组卷：51引用：1难度：0.8

  解析

• 4．已知

  0

  ＜

  α

  ＜

  π

  2

  ，

  cos

  （

  α

  +

  π

  6

  ）

  =

  -

  2

  5

  ，则

  tan

  （

  5

  π

  6

  -

  α

  ）

  =（　　）

  A． 5 2

  B． - 21 2

  C． 21 2

  D． - 5 3
  组卷：123引用：1难度：0.7

  解析

• 5．已知△ABC的外接圆半径为1，

  A

  =

  π

  3

  ，则AC•cosC+AB•cosB=（　　）

  A． 1 2

  B．1

  C． 3 2

  D． 3
  组卷：345引用：3难度：0.7

  解析

• 6．已知向量

  a

  、

  b

  满足

  |

  a

  |

  =

  2

  ，

  |

  b

  |

  =

  2

  ，

  a

  •

  b

  =

  -

  2

  ，设

  a

  与

  a

  +

  b

  的夹角为θ，则cosθ=（　　）

  A． 1 2

  B． - 1 2

  C． 2 2

  D． - 2 2
  组卷：139引用：3难度：0.5

  解析

• 7．函数y=tan（

  1

  2

  x

  -

  1

  3

  π

  ）在一个周期内的图象是（　　）

  A．	B．
  C．	D．
  组卷：3224引用：20难度：0.9

  解析

四、解答题（本大题共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤）

• 21．已知向量

  a

  =

  （

  cosx

  ,

  cosx

  ）

  ，

  b

  =

  （

  cosx

  ,

  3

  sinx

  ）

  ，函数

  f

  （

  x

  ）

  =

  2

  a

  •

  b

  ，x∈R．
  （1）求函数f（x）的最小正周期、值域；
  （2）对任意实数x₁，x₂，定义

  max

  {

  x

  1

  ，

  x

  2

  }

  =

  x 1 ， x 1 ≥ x 2 ，

  x 2 ， x 1 ＜ x 2 .

  设

  g

  （

  x

  ）

  =

  max

  {

  3

  asinx

  ,

  acosx

  }

  ，x∈R，a为大于0的常数，若对于任意x₁∈R，总存在x₂∈R，使得g（x₁）=f（x₂）恒成立，求实数a的取值范围．
  组卷：39引用：1难度：0.6

  解析

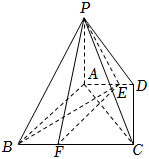• 22．如图，在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，∠ADC=90°，AD∥BC，AB⊥AC，AB=AC=

  2

  ，E点在AD上，且AE=2ED．
  （1）已知点F在BC上，且CF=2FB，求证：平面PEF⊥平面PAC；
  （2）求点D到平面PAB的距离．
  组卷：119引用：4难度：0.6

  解析